даю 50 баллов решите систему неравенств
-x²+2x+8<0
6-2(x+1)>2x
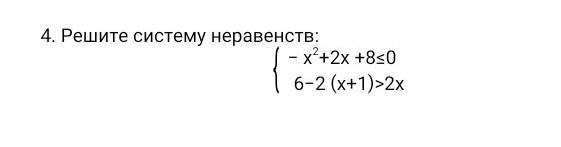
Ответы
Ответ:
Решим систему неравенств по очереди:
-x² + 2x + 8 < 0
Для начала найдем корни квадратного уравнения -x² + 2x + 8 = 0. Используя формулу дискриминанта, получим:
D = (2)² - 4(-1)(8) = 4 + 32 = 36
D > 0, поэтому у уравнения есть два различных корня. Мы можем решить уравнение, поставив его равным нулю:
-x² + 2x + 8 = 0
Применяя метод решения квадратных уравнений, получим:
x₁ = (-2 + √D) / -2 = (-2 + √36) / -2 = (-2 + 6) / -2 = 4 / -2 = -2
x₂ = (-2 - √D) / -2 = (-2 - √36) / -2 = (-2 - 6) / -2 = -8 / -2 = 4
Таким образом, корни уравнения равны x₁ = -2 и x₂ = 4.
Чтобы определить, в каких интервалах выполняется неравенство -x² + 2x + 8 < 0, построим таблицу знаков:
| -x² + 2x + 8
x < -2 | -
-2 < x < 4 | +
x > 4 | -
Из таблицы видно, что неравенство -x² + 2x + 8 < 0 выполняется в интервале -2 < x < 4.
6 - 2(x + 1) > 2x
Упростим неравенство:
6 - 2x - 2 > 2x
4 > 4x
x < 1
Таким образом, второе неравенство выполняется при x < 1.
Итак, решением системы неравенств будет интервал -2 < x < 1.
Объяснение: