СРОЧНО!!! ДОПОМОЖІТЬ БУДЬ ЛАСКА!!! БЛАГАЮ!!!
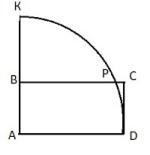
На малюнку зображено прямокутник АВСD і сектор КАD, площа якого дорівнює 156,25 π. Дуга КD перетинає сторону ВС у точці Р, ВР=24. Знайдіть: довжину AD, довжину CD, периметр трикутника KBP.
Буду дуже безмежно вдячний вам.
Ответы
Відповідь:
Для розв'язання цієї задачі спочатку знайдемо радіус та центр сектора КАD. Зауважимо, що площа сектора обчислюється за формулою S = (1/2) * r^2 * α, де S - площа сектора, r - радіус, α - центральний кут в радіанах.
156.25π = (1/2) * r^2 * α
Оскільки ми знаємо, що дуга КD перетинає сторону ВС у точці Р і ВР = 24, ми можемо знайти кут ВКР. Зауважимо, що цей кут дорівнює половині центрального кута KD, оскільки ВР є радіусом, що розділяє цей центральний кут навпіл.
Таким чином, α = 2 * кут ВКР.
Оскільки ВР = 24 і ВК = 2 * ВР = 48, ми маємо трикутник ВКР зі сторонами 24, 48 і ВК, для якого можна застосувати теорему косинусів:
ВК^2 = ВР^2 + ВР^2 - 2 * ВР * ВР * cos(ВКР).
Підставимо відомі значення:
ВК^2 = 24^2 + 24^2 - 2 * 24 * 24 * cos(ВКР).
ВК^2 = 576 + 576 - 2 * 576 * cos(ВКР).
ВК^2 = 1152 - 1152 * cos(ВКР).
Тепер ми можемо обчислити довжину ВК.
Знаючи довжину ВК, ми можемо знайти радіус r:
r = ВК / 2.
Знаючи радіус, ми можемо знайти довжину AD:
AD = 2 * r.
І, нарешті, ми можемо обчислити довжину CD:
CD = 2 * r * sin(α/2).
Периметр трикутника KBP складається з суми сторін KB, BP і ВК.
Застосовуючи ці формули, ми зможемо знайти шукані значення.