Предмет: Геометрия,
автор: daaddddq
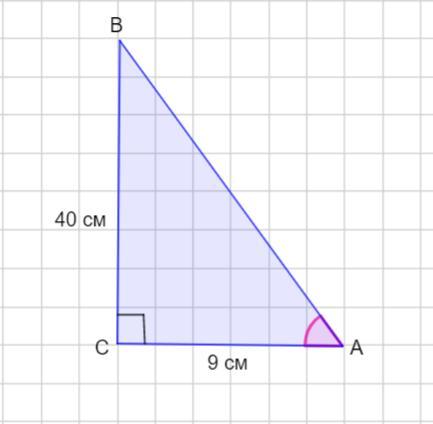
В треугольнике ABC ∠C = 90°, BС = 40 см, AC = 9 см. Найдите: 1) cos А;
2) tg A.
Ответы
Автор ответа:
1
Ответ:
Объяснение:
В треугольнике АВС ∠С =90°, ВС =40 см, АС = 9 см.
Найти: 1) cosA; 2) tgA.
ΔABC - прямоугольный . Катеты ВС =40 см, АС = 9 см. Найдем гипотенузу по теореме Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
АВ² = ВС² +АС²
АВ² = 40² +9² = 1600 + 81 =1681;
АВ = √1681 = 41 см.
Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему катета .
#SPJ1
Приложения:
Похожие вопросы
Предмет: История,
автор: mariaemec8
Предмет: Математика,
автор: arinovmejrzan47
Предмет: Английский язык,
автор: levakirichenko
Предмет: Математика,
автор: lastdayonertz1
Предмет: Химия,
автор: kiiloov