Предмет: Алгебра,
автор: KatyaTyu123
Помогите пожалуйста с одним примером
Приложения:
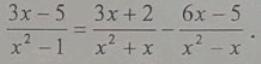
Ответы
Автор ответа:
1
Второй корень не подходит
Ответ: х = - 0,5
Похожие вопросы
Предмет: Литература,
автор: Glgllglglgl
Предмет: Геометрия,
автор: whynottsss
Предмет: Физика,
автор: yuliakalashnikova202
Предмет: Українська мова,
автор: biliknasta02117
Предмет: Математика,
автор: Аноним