3. Решите систему неравенств: 5x- 12 < 0 13x²-7x +4 20
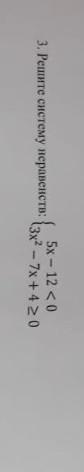
Ответы
Из заданной системы неравенств выделим каждое неравенство и решим их по отдельности:
5x - 12 < 0
Добавим 12 к обеим частям неравенства:
5x < 12
Разделим обе части на 5, сохраняя знак неравенства:
x < 12/5
13x² - 7x + 4 < 20
Перенесем все слагаемые в левую часть неравенства:
13x² - 7x - 16 < 0
Решим квадратное уравнение:
x1 = (7 + √(7² + 4·13·16)) / (2·13) ≈ 1,45
x2 = (7 - √(7² + 4·13·16)) / (2·13) ≈ -1,05
Теперь осталось проверить выполнение условия в исходном неравенстве:
13x² - 7x + 4 < 20
Для x1: 13·(1,45)² - 7·1,45 + 4 ≈ 5,54 < 20 - неравенство выполняется
Для x2: 13·(-1,05)² - 7·(-1,05) + 4 ≈ 2,84 < 20 - неравенство выполняется
Таким образом, решением системы неравенств является множество всех x, меньших 12/5, и лежащих в интервале между x1 и x2:
{x: x < 12/5, -1.05 < x < 1.45}