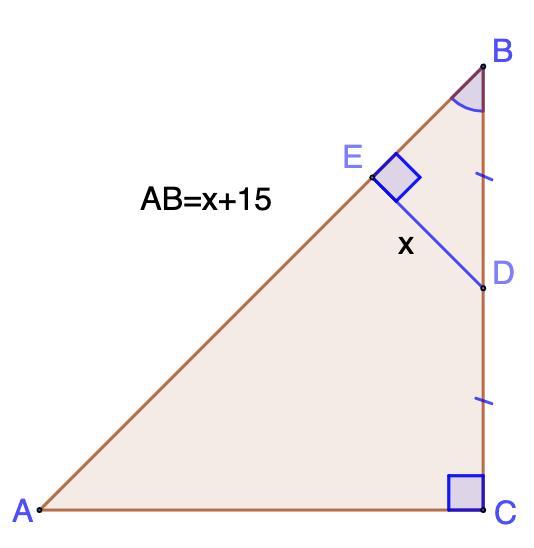
Точка Д- середина катета ВС рівнобедреного прямокутного трикутника АВС<С=90°. Відстань від точки Д до гепотинузи трикутника на 15см менша від гіпотенузи. Знайдіть гіпотезу трикутника
Ответы
Ответ:
Гипотенуза треугольника равна 20 см.
Объяснение:
Точка D - середина катета ВС равнобедренного прямоугольного треугольника АВС. ∠C = 90°. Расстояние от точки D до гипотенузы треугольника на 15 см меньше гипотенузы. Найдите гипотенузу треугольника.
Дано: ΔАВС - прямоугольный, равнобедренный;
∠С = 90°;
D ∈ BC; BD = DC;
DE - расстояние от D до АВ;
AB = DE + 15 (см).
Найти: АВ.
Решение:
- Расстояние от точки до прямой - длина перпендикуляра, опущенного из данной точки на данную прямую.
⇒ DE ⊥ AB
Пусть DE = x см, тогда АВ = (х + 15) см.
Рассмотрим ΔАВС - прямоугольный, равнобедренный;
- Углы при основании равнобедренного треугольника равны.
⇒ ∠А = ∠В
- Сумма острых углов прямоугольного треугольника равна 90°.
⇒ ∠А = ∠В = 90° : 2 = 45°
Рассмотрим ΔDEB - прямоугольный.
∠ЕDВ = 90° - ∠B = 90° - 45° = 45°
- Если в треугольнике два угла равны, то он равнобедренный.
⇒ DE = EB = x см.
По теореме Пифагора:
- Квадрат гипотенузы равен сумме квадратов катетов.
BD² = DE² + EB² = 2x² ⇒ BD = √2 · х см
⇒ BD = DC = √2 · x см, ВС = АС = 2√2 ·х (см)
По теореме Пифагора из ΔАВС:
АВ² = ВС² + АС²
(х + 15)² = 8х² + 8х²
х² + 30х + 225 = 16х²
15х² - 30х - 225 = 0 |:15
x² - 2x - 15 = 0
D = 4 + 60 = 64 ⇒ √D = 8
x₁ = (2 + 8)/2 = 5; x₂ = (2 - 8)/2 = -3
x₂ - не подходит по условию задачи.
⇒ DE = 5 см
Тогда АВ = 5 + 15 = 20 (см)
Гипотенуза треугольника равна 20 см.
#SPJ1