Question

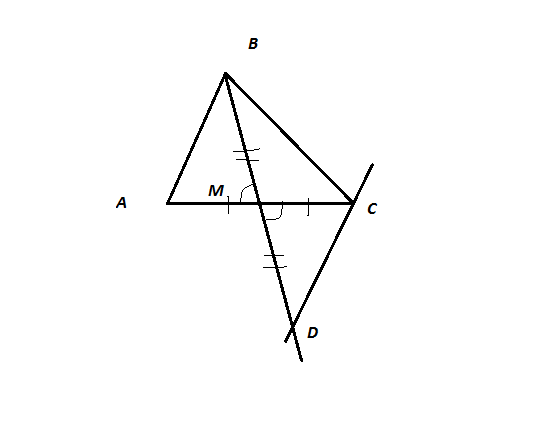
В  треугольнике  АВС  медиана  ВМ  продолжается  за  точку  М  так,  что  ВМ=MD. 
Докажите параллельность прямых АВ и DC.   Как мне в данном случае сделать рисунок?                                            

Answer 1

Получившиеся треугольники АВМ и МDС равны по первому признаку равенства треугольников: если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
В нашем случае:
АМ = МС, т.к. ВМ - медиана,
ВМ = MD по условию,
углы АМВ и DМС равны как вертикальные углы.
Следовательно, треугольники АВМ и МDС полностью совместятся при наложении, и АВ II CD

Answer 2

спасибо за рисунок и решение)