Question

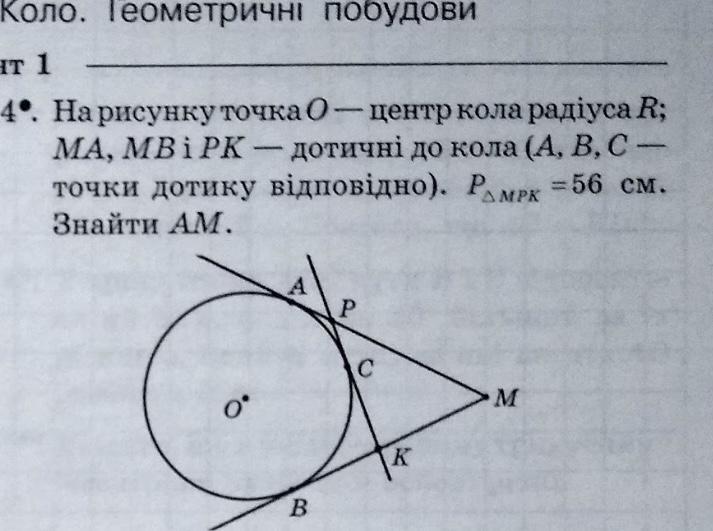
На рисунку точка О - центр кола радіуса R;
MA, MBIPK - дотичні до кола (A, B. С - точки дотику відповідно). Ромрх =56 см. Знайти АМ

Answer 1

Ответ:

Для решения этой задачи мы воспользуемся свойствами касательных-касательные к окружности,проведённые из точки вне окружности,равны между собой

Смотри на чертёж

АМ=ВМ,их провели из точки М

ВК=СК,их провели из точки К

АР=РС,их провели из точки Р

Теперь посмотри на треугольник РКМ

Сторона РК состоит из отрезков,которые отсекли от касательных АМ и МВ

Отрезок АР отсекли от касательной АМ

АР=РС,поэтому одна часть стороны РК равна АР

От касательной ВМ отсекли отрезок ВК

ВК=СК,а это вторая часть стороны РК

Если сторону РК разобрать на составляющие и вернуть на место-к секущим АМ и МВ,то окажется,что

АМ+МВ=56 см

АМ=МВ=56:2=28 см

Объяснение: