Предмет: Алгебра,
автор: maxzas326
ДОПОМОЖІТЬ!!!! ДУЖЕ ПРОШУ!!!!
Приложения:
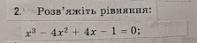
Ответы
Автор ответа:
1
Ответ:
Решить уравнение .
Так как при подстановке вместо х числа 1 уравнение обращается в верное равенство, то х=1 - корень уравнения . Значит, можно нацело разделить многочлен на разность (х-1) .
Действительно, .
Значит, .
Теперь найдём корни квадратного трёхчлена .
Ответ:
Приложения:


Похожие вопросы
Предмет: География,
автор: vovasima2009
Предмет: Математика,
автор: Аноним
Предмет: Химия,
автор: Chill253
Предмет: История,
автор: Pingvinarestokrat