Question

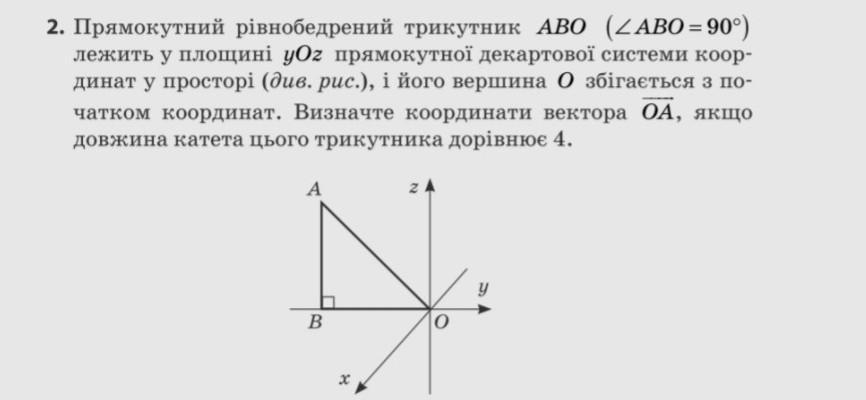
Срочно, помогите пожалуйста!!!Прямокутний рівнобедрений трикутник ABO (<ABO = 90º) лежить у площині у г прямокутної декартової системи коор динат у просторі (див. рис.), і його вершина О збігається з по- чатком координат. Визначте координати вектора ОА, якщо довжина катета цього трикутника дорівнює 4.​

Answer 1

Ответ:

$\tt \vec {OA}$ = (0; -4; 4)

Объяснение:

Перевод: Прямоугольный равнобедренный треугольник ABO (∠ABO = 90º) лежит в плоскости уOz прямоугольной декартовой системы координат в пространстве (см. рис.), и его вершина О совпадает с началом координат. Определите координаты вектора $\tt \vec {OA}$, если длина катета этого треугольника равна 4.

Решение. Определим координаты точки A(x; y; z). Треугольник ABO полностью лежит в плоскости уOz, что означает x = 0.

По условию BO = 4, отсюда y = -4 - так как проекция точки A попадает в отрицательную часть оси Oy и лежит на расстоянии 4 единиц от начала координат.

Далее, в силу того, что треугольник равнобедренный AB = BO = 4. Но проекция точки A на ось Oz равна лежит на расстоянии 4 единиц от начала координат в положительном направлении, то есть z = 4

Значит, координатами точки A будут (0; -4; 4).

Вектор $\tt \vec {OA}$ определяется как разность координат точек A и O:

$\tt \vec {OA}$ = (0-0; -4-0; 4-0) = (0; -4; 4).

#SPJ1