Предмет: Алгебра,
автор: Patrokl
Решите систему показательных уравнений:
Приложения:
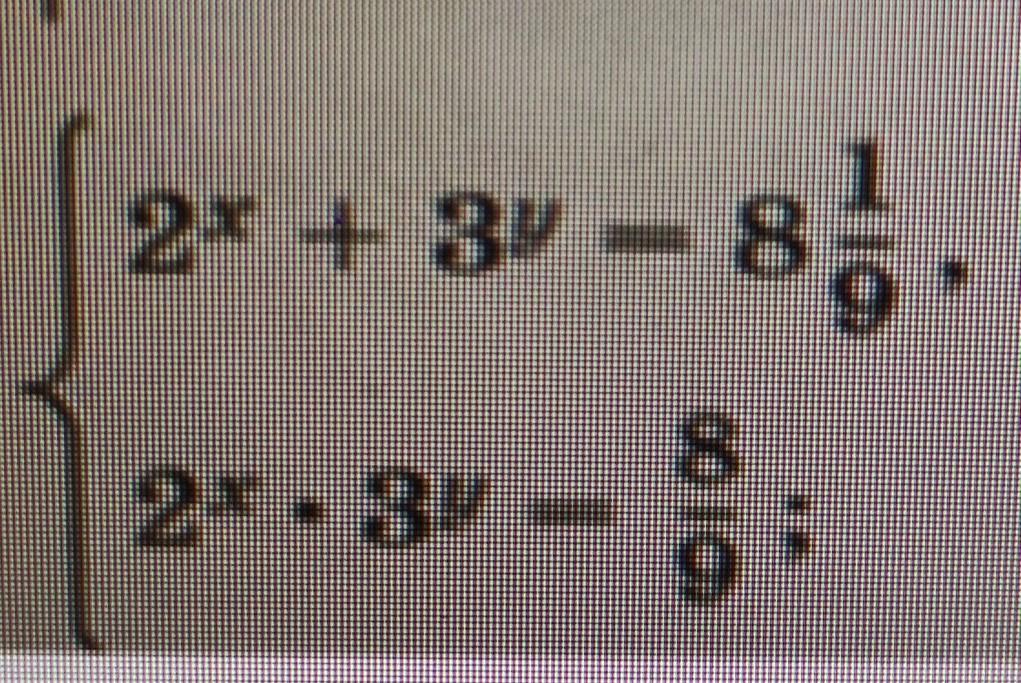
Ответы
Автор ответа:
1
Ответ:
Решаем с помощью замены переменных .
Вернёмся к старым переменным .
Приложения:

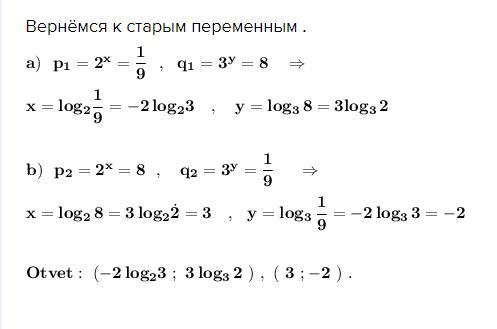
Michael12341:
прошу вас, помогите пожалуйста с алгеброй у меня в профиле
очень нужна ваша помощь, прошу, пожалуйста
Похожие вопросы
Предмет: Алгебра,
автор: Аноним
Предмет: Геометрия,
автор: vikakkk56
Предмет: Математика,
автор: fetkosemen
Предмет: Физика,
автор: amelinevgenij9
Предмет: Русский язык,
автор: vilzepuzz