Предмет: Геометрия,
автор: Аноним
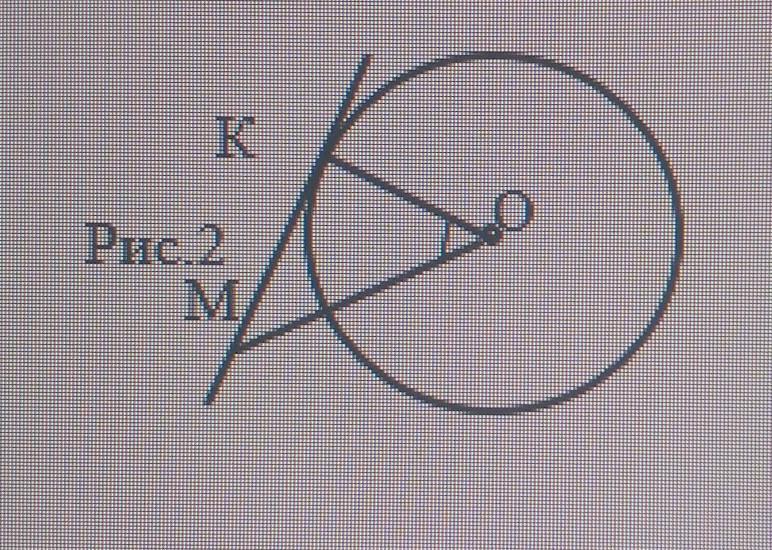
2. К окружности с центром в точке О проведена касательная МК (рис. 2). Найдите отрезок ОМ, если радиус окружности равен 2,4 см и угол КОМ = 45°
Приложения:
Ответы
Автор ответа:
1
Радиус в точку касания перпендикулярен касательной.
OK⊥MK, ∠MKO=90°
Рассмотрим прямоугольный треугольник MKO
∠KMO=90°-KOM =90°-45° =45°
=> ∠KMO=∠KOM=45°
△MKO - равнобедренный (т.к. углы при основании равны)
MK=OK=x, т Пифагора:
OM =√(MK^2 +OK^2) =√(2x^2) =x√2
Ответ: OM =OK√2 = 2,4 √2 (см)
-----------------------------------------------------
В треугольнике с углами 45°, 90° (прямоугольный равнобедренный) стороны относятся как 1 : 1 : √2
siestarjoki:
2,4 √2
примерно 3,4
Похожие вопросы
Предмет: История,
автор: voloshanivskad
Предмет: История,
автор: kikidrww
Предмет: Физика,
автор: anastasialazorik748
Предмет: Биология,
автор: starayasolomiya
Предмет: Русский язык,
автор: senashukurov