Предмет: Геометрия,
автор: anastasiaspivak24200
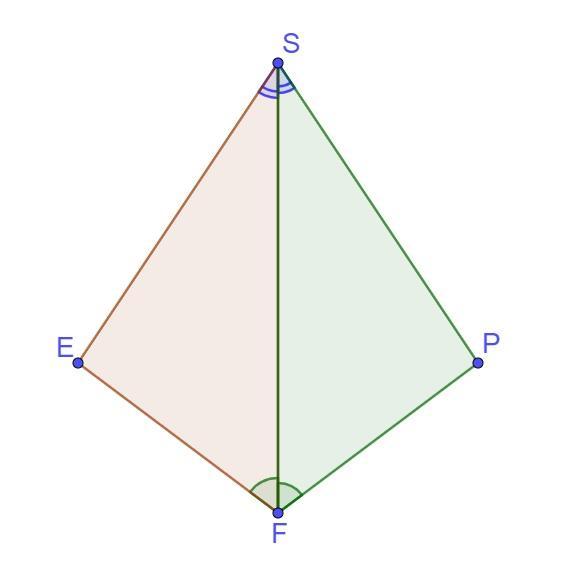
Два трикутники ESF і PSF мають спільну сторону SF , причому FS - бісектриса ∠EFP , SF - бісектриса ∠ESP . Довести, що ∠E = ∠P .
БУДЬ ЛАСКА !!!
З МАЛЮНКОМ
І ДАНО
Ответы
Автор ответа:
1
Ответ:
Довели, що ∠E = ∠P
Объяснение:
Два трикутники ESF і PSF мають спільну сторону SF , причому FS - бісектриса ∠EFP , SF - бісектриса ∠ESP . Довести, що ∠E = ∠P
- Бісектриса кута — промінь, що проходить через вершину кута і ділить його навпіл.
Друга ознака рівності трикутників — за стороною й прилеглими до неї кутами:
- Якщо сторона й прилеглі до неї кути одного трикутника дорівнюють відповідно стороні й прилеглим до неї кутам другого трикутника, то такі трикутники рівні.
Дано: ΔESF і ΔPSF, FS - бісектриса ∠EFP , SF - бісектриса ∠ESP
Довести: ∠E = ∠P
Доведення
Розглянемо ΔESF і ΔPSF.
Так як FS - бісектриса ∠EFP, то за означенням бісектриси: ∠EFS=∠PFS
Так як SF - бісектриса ∠ESP, то за означенням бісектриси: ∠ESF=∠PSF
SF - спільна сторона
Отже, ΔESF = ΔPSF за стороною й прилеглими до неї кутами (2 ознака).
Зрівності трикутників ⇒ ∠E = ∠P
Довели.
#SPJ1
Приложения:
anastasiaspivak24200:
чооооо
здравствуйте, помогите пожалуйста с геометрией, там две части умоляю!)
Похожие вопросы
Предмет: Физкультура и спорт,
автор: Аноним
Предмет: Физика,
автор: asazazs087
Предмет: Українська література,
автор: ThePandochka
Предмет: Українська література,
автор: Whoffgg
Предмет: Литература,
автор: nastia300308