Question

a) 2x+y=12, 7x-2y=31; 6) | y-2x=4, 7x-y=1; B) { 8y-x=4, 2x-21y=2; r) 2x=y+0,5, 3x-5y=13. { 2.
​

Answer 1

Ответ:

там сверху есть подробней как делаеться но скрин неделает всё но ответ виден перепиши ответ и всё

Пошаговое объяснение:

надеюсь помог УДАЧИ!!!

Answer 2

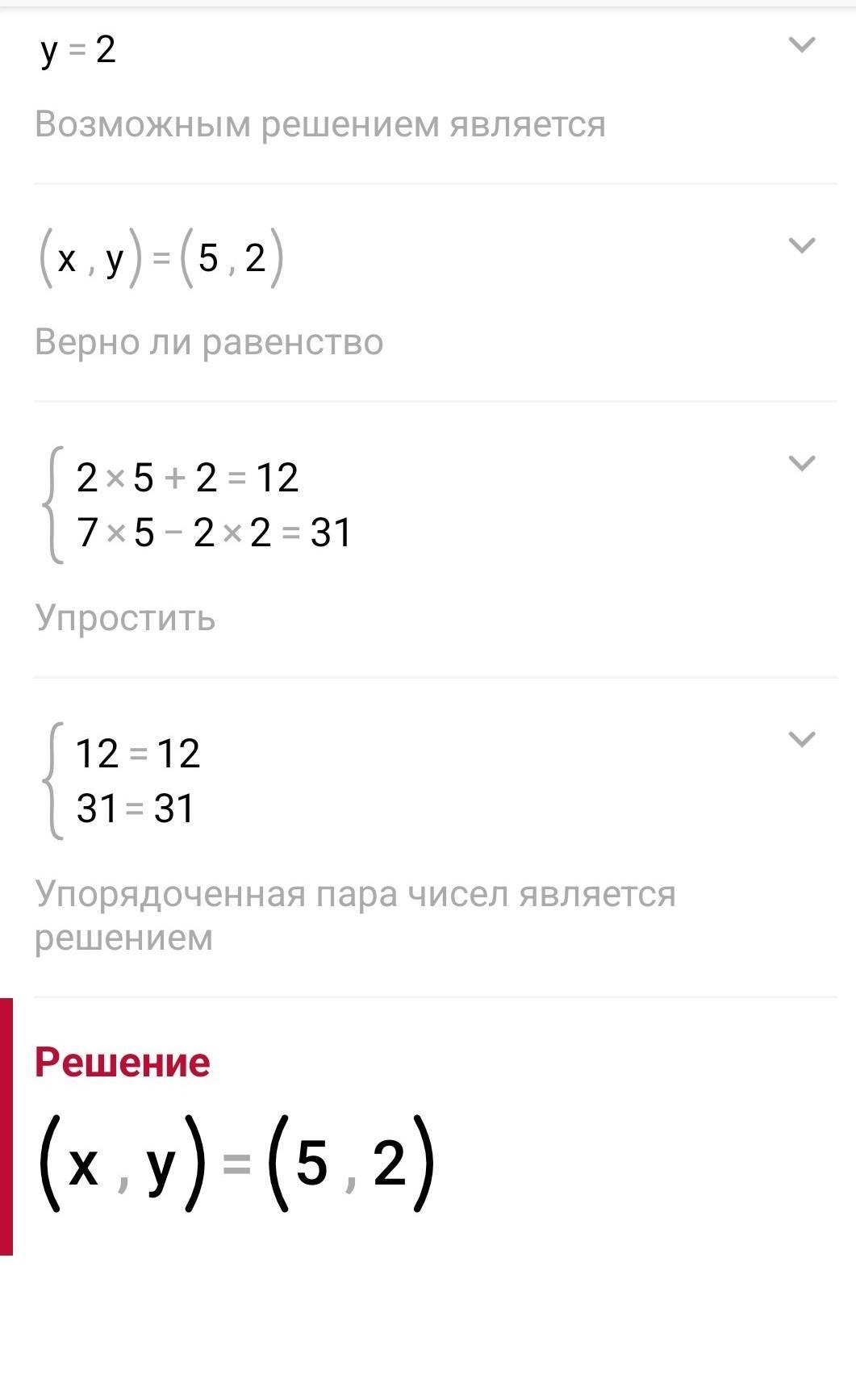
Ответ:

a) To solve this system of equations, we can use either substitution or elimination method. Let's use elimination method:

2x + y = 12

7x - 2y = 31

To eliminate y, we can multiply the first equation by 2 and add it to the second equation:

4x + 2y = 24

7x - 2y = 31

-------------

11x = 55

Dividing both sides by 11, we get:

x = 5

Now we can substitute x = 5 into either equation to find y. Let's use the first equation:

2x + y = 12

2(5) + y = 12

10 + y = 12

y = 2

Therefore, the solution to this system of equations is (x, y) = (5, 2).

6) To solve this system of equations, we can use either substitution or elimination method. Let's use substitution method:

| y - 2x = 4

| 7x - y = 1

From the first equation, we can solve for y:

y = 2x + 4

Now we can substitute this expression for y into the second equation:

7x - y = 1

7x - (2x + 4) = 1

5x = 5

x = 1

Substituting x = 1 into the first equation, we can find y:

y - 2x = 4

y - 2(1) = 4

y = 6

Therefore, the solution to this system of equations is (x, y) = (1, 6).

B) To solve this system of equations, we can use either substitution or elimination method. Let's use elimination method:

8y - x = 4

2x - 21y = 2

To eliminate x, we can multiply the first equation by 2 and add it to the second equation:

16y - 2x = 8

2x - 21y = 2

--------------

-5y = 10

Dividing both sides by -5, we get:

y = -2

Now we can substitute y = -2 into either equation to find x. Let's use the first equation:

8y - x = 4

8(-2) - x = 4

-16 - x = 4

x = -20

Therefore, the solution to this system of equations is (x, y) = (-20, -2).

r) To solve this system of equations, we can use either substitution or elimination method. Let's use substitution method:

2x = y + 0.5

y = 2x - 0.5

Now we can substitute this expression for y into the second equation:

3x - 5y = 13

3x - 5(2x - 0.5) = 13

3x - 10x + 2.5 = 13

-7x = 10.5

x = -1.5

Substituting x = -1.5 into the first equation, we can find y:

2x = y + 0.5

2(-1.5) = y + 0.5

-3 - 0.5 = y

y = -3.5

Therefore, the solution to this system of equations is (x, y) = (-1.5, -3.5).