Question

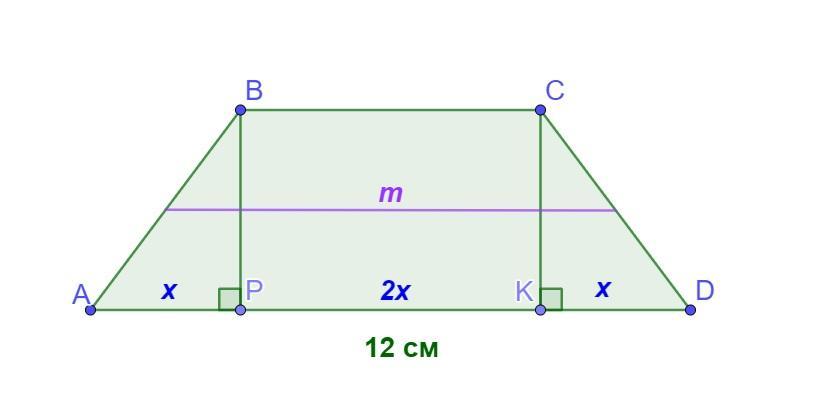
Висоти, проведені з вершини меншої основи рівнобічної трапеції, ділять більшу основу на три відрізки, сума двох з яких дорівнює третьому. Більша основа трапеції дорівнює 12 см, а її середня лінія - висоті трапеції. Знайти площу трапеції

Answer 1

Ответ:

Площа трапеції ABCDдорівнює 81 см²

Пошаговое объяснение:

Висоти, проведені з вершин меншої основи рівнобічної трапеції, ділять більшу основу на три відрізки, сума двох з яких дорівнює третьому. Більша основа трапеції дорівнює 12 см, а її середня лінія - висоті трапеції. Знайти площу трапеції

Середня лінія трапеції рівна півсумі основ, тому формулу площі трапеції можна записати у вигляді:

S=m·h

де m - середня дінія трапеції,  h - її висота.

Так як за умовою m=h, то площу трапеції будемо знаходити за формулою:

S=m²

Розв'язання

1) Нехай дано рівнобічну трапецію ABCD, BC║AD, АВ=CD, АD=12 см.

Проведемо висоти ВР і СК. ВР⊥АD, СК⊥АD.

Розглянемо ΔАВР і ΔDСК.

• ∠АРВ=∠DКС=90°

• ВР=СК (висоти)

• АВ=СD (трапеція рівнобока)

Отже, ΔАВР = ΔDСК (за катетом і гіпотенузою), з цього випливає, що АР=КD.

2) Оскількі АР=КD, то АР+КD=РК.

Позначимо АР=КD=х, тоді РК=2х.

Отже за аксиомою вимірювання відрізків: АD=АР+РК+КD=х+2х+х=4х

Маємо: 4х=12, х=3.

РК=2х=2·3=6 (см)

3) Оскільки ВСКР - прямокутник (ВС║РК, ВР=СК, ВР⊥АD, СК⊥АD), то ВС=РК= 6 (см)

4) Знайдемо середню лінію трапеції:

$\sf m=\dfrac{BC+AD}{2} =\dfrac{6+12}{2} =\bf 9$   (см)

5) Площа трапеції ABCD:

S=m²=9²=81 (cм²)

Відповідь: 81 см²

#SPJ1