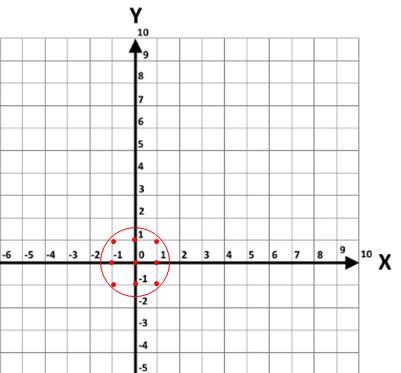
867. В координатной плоскости построен круг радиуса 1,5 с центром
в начале координат. Какова вероятность того, что наудачу взя-
тая точка этого круга с целочисленными координатами является
его центром?
Ответы
Ответ:
Вероятность того, что наудачу взятая точка этого круга с целочисленными координатами является его центром равна
Объяснение:
Информация: Вероятностью события A в некотором испытании называют отношение: P (A) = m/n, где n - общее число всех равно возможных, элементарных исходов этого испытания, а m - количество элементарных исходов, благоприятствующих событию A.
Решение. Радиус круга 1,5 и с центром в начале координат. Тогда следующие 5 точек с целочисленными координатами принадлежать кругу:
(-1; 0), (0; 0), (1; 0), (0; -1), (0; 1).
Далее, так как то следующие 4 точки с целочисленными координатами также принадлежать кругу:
(-1; -1), (-1; 1), (1; 1), (1; -1).
Значит, количество точек с целочисленными координатами всего 9 и нужная точка только 1. Тогда вероятность того, что наудачу взятая точка этого круга с целочисленными координатами является его центром равна
#SPJ1