Question

Периметр трикутника дорівнює 140 см. Одна зі сторін трикутника ділиться точкою дотику вписаного в трикутник кола на відрізки 15 см і 20 см. Знайди дві інші сторони трикутника.

Answer 1

Ответ:

Дві інші сторони трикутника дорівнюють 50 см і 55 см

Объяснение:

Периметр трикутника дорівнює 140 см. Одна зі сторін трикутника ділиться точкою дотику вписаного в трикутник кола на відрізки 15 см і 20 см. Знайди дві інші сторони трикутника.

• Відрізки дотичних, проведених з однієї точки до кола, рівні.

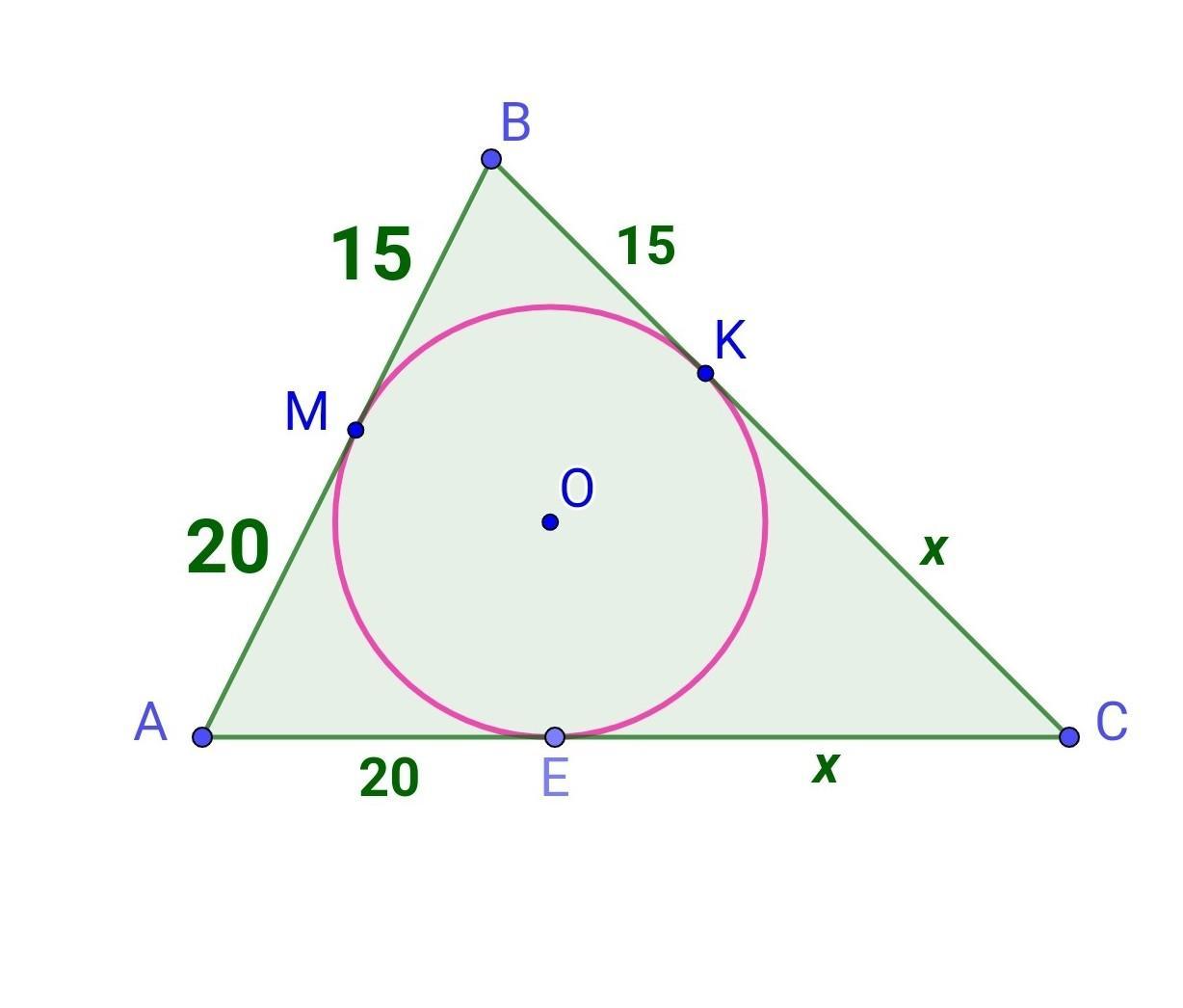
Маємо △АВС, коло з центром в точці О, вписане у △АВС, т.М, К, Е - точки дотику.

АМ=20 см, ВМ=15 см. Периметр △АВС дорівнює 140 см. Знайдемо ВС і АС.

ВК=ВМ=15 (см); АЕ=АМ=20 (см); СЕ=СК - як відрізки дотичних, проведених з точки до кола.

Нехай СЕ=СК=х (см). Тоді за аксиомою вимірювання відрізків отримаємо:

ВС=ВК+СК=15+х;

АС=АЕ+СЕ=20+х.

АВ=АМ+ВМ=20+15=35.

Периметр трикутника дорівнює сумі всіх його сторін:

Р(АВС)=АВ+ВС+АС

35+15+х+20+х=140

2х=140-70

х=70:2

х=35

Отже, ВС=15+35=50(см), АС=20+35=55(см).

Відповідь: 50 см, 55 см

#SPJ1