Предмет: Геометрия,
автор: Аноним
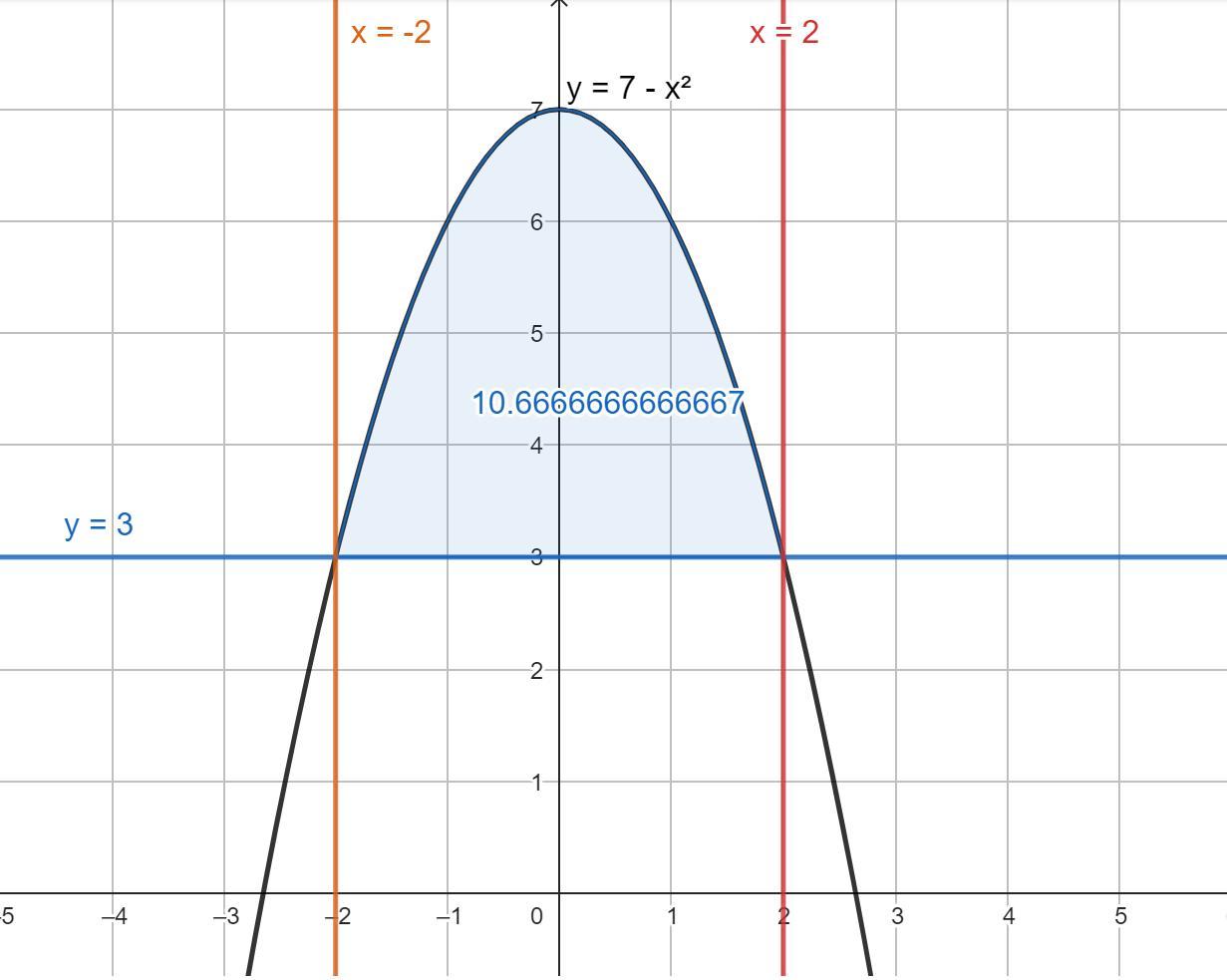
Обчисліть площу фігури, обмеженої параболою
y =7-x^2 i прямою y = 3.
Ответы
Автор ответа:
3
Ответ:
S = 10 2/3 (ед)²
Объяснение:
Найдем точи пересечений данных графиков
7 - x² = 3
x² = 4
Находим площадь фигуры
(ед)²
Приложения:
Drudiller222:
Учитель побачив що в сайті є відповідь і поставив 0 балів((((
Та же проблема, тепер учителя создають свої питання і потім чекають цей сайт, мені теж 1 прилетіла
Похожие вопросы
Предмет: Английский язык,
автор: darinamatenova9
Предмет: Химия,
автор: seredadasha0110
Предмет: Математика,
автор: varvara312022
Предмет: Математика,
автор: guslen290822