Предмет: Математика,
автор: VitalyKotuk
Обчислити означені інтеграли Варіант 6 а) і б).
Приложения:

Ответы
Автор ответа:
1
Ответ:
a) Замена переменной (подстановка) , выделение дифференциала функции .
б) Интегрирование по частям : .
Приложения:

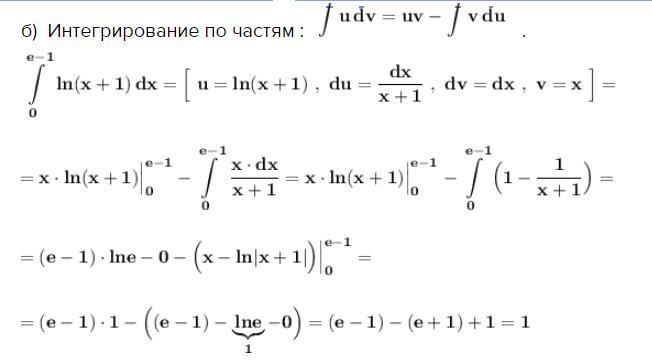
Похожие вопросы
Предмет: История,
автор: e7206108
Предмет: История,
автор: misenkoangelina27
Предмет: Химия,
автор: annavolui12
Предмет: Английский язык,
автор: zhanibekuli13