Question

найдите все значения a, при каждом из которых уравнение имеет хотя бы один корень, принадлежащий промежутку [-2; 1)

Answer 1

Ответ:

$\displaystyle\bf a\in [-4; 2)\cup\bigg(2;2\frac{1}{4}\bigg]$

Объяснение:

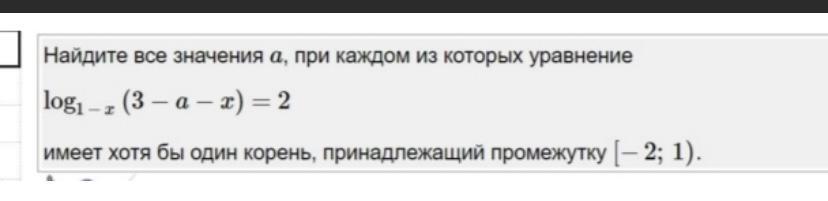
Найдите все значения a, при каждом из которых уравнение

$\displaystyle\bf log_{1-x}(3-a-x)=2$

имеет хотя бы один корень, принадлежащий промежутку [-2; 1).

• Определение логарифма:

   $\displaystyle\bf log_ab=x\;\;\;\iff\;\;\;a^x=b,\;\;\;a > 0;\;a\neq 1;\;b > 0$

⇒ Данное уравнение равносильно системе:

$\begin{equation*} \begin{cases} (1-x)^2=3-a-x \\1-x\neq 1 \\1-x > 0 \end{cases}\;\;\;\iff\;\;\;\begin{equation*} \begin{cases}1-2x+x^2-3+a+x=0 \\x\neq 0 \\x < 1 \end{cases}\end{equation*}$

$\begin{equation*} \begin{cases}x^2-x+a-2=0 \\x\neq 0 \\x < 1 \end{cases}$

Так как x ≠ 0, то данный промежуток  [-2; 1) разделится на два промежутка: [-2; 0) и (0; 1).

То есть, система имеет хотя бы один корень на промежутке [2;1), если уравнение   $\displaystyle log_{1-x}(3-a-x)=2$   имеет хотя бы один корень на промежутках [-2; 0) или (0; 1).

График функции f(x) = x² - x + a - 2 - парабола, ветви вверх.

Абсцисса вершины:

$\displaystyle x_0=-\frac{-1}{2} =\frac{1}{2}$

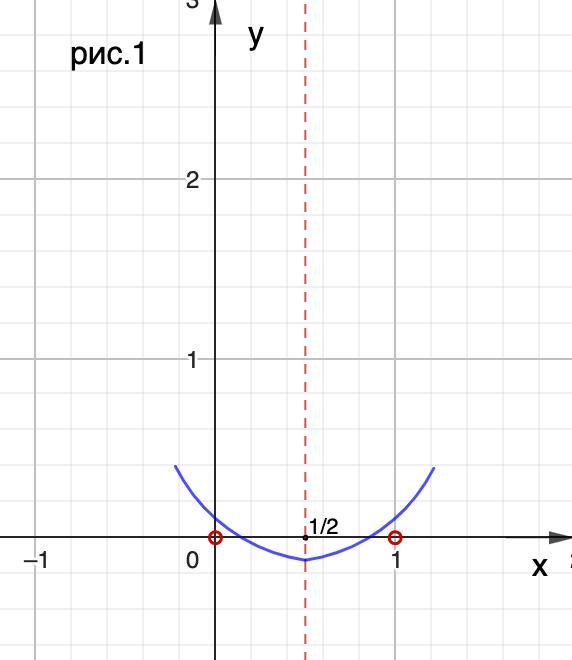
Рассмотрим промежуток (0; 1) (Рис. 1).

Уравнение f(x) = 0 будет иметь хотя бы один корень, если вершина будет лежать ниже или на оси Ох, а точки, а точки f(0) = f(1) выше оси Ох.

$\displaystyle \left \{ {{f(\frac{1}{2}) \leq 0} \atop {f(0)=f(1) > 0}} \right. \;\;\;\iff\;\;\left \{ {{\frac{1}{4}-\frac{1}{2} +a-2\leq 0} \atop {a-2 > 0}} \right. \;\;\;\iff\;\;\;\left \{ {{a\leq 2\frac{1}{4} } \atop {a > 2}} \right.$

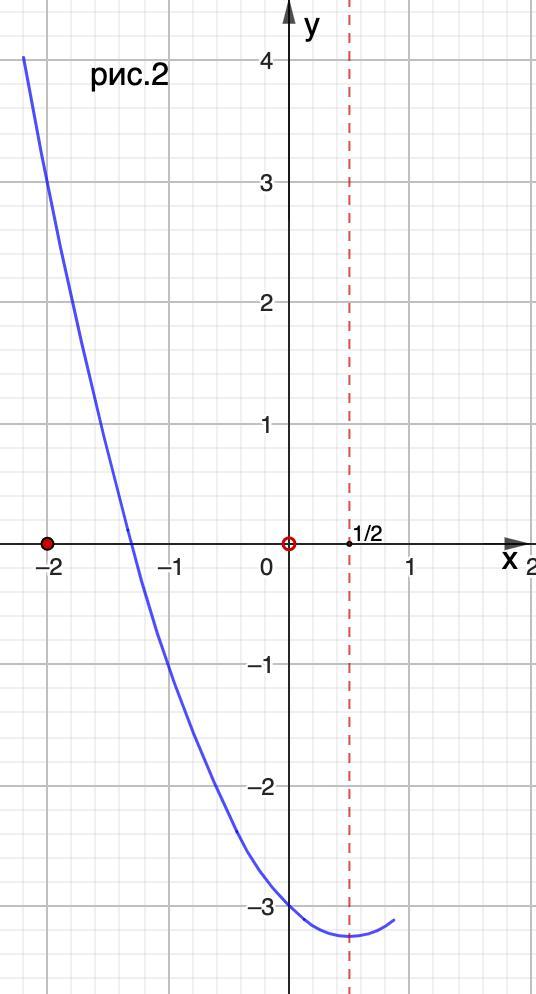
Рассмотрим промежуток [-2; 0) (Рис. 2).

Здесь уравнение f(x) = 0 будет иметь хоть один корень, если f(-2) ≥ 0, а f(0) < 0. То есть, ветвь параболы должна пересечь ось Ох.

$\displaystyle \left \{ {{f(-2)\geq 0} \atop {f(0) < 0}} \;\;\;\iff\;\;\;\right. \left \{ {{4+2+a-2\geq 0} \atop {a-2 < 0}} \right. \;\;\;\iff\;\;\;\left \{ {{a\geq -4} \atop {a < 2}} \right.$

Ответ:    $\displaystyle [-4; 2)\cup\bigg(2;2\frac{1}{4}\bigg]$

#SPJ1