Предмет: Алгебра,
автор: Оляя1995
Вычислите площадь фигуры, ограниченной линиями y = 4x-x (в квадрате), y = 4-x.
Ответы
Автор ответа:
0
Найдем пределы интегрирования
4х-х²=4-х
х²-5х+4=0
х1+х2=5 и х1*х2=4
х1=1 и х2=4
Фигура ограничена сверху параболой,а снизу прямой


4х-х²=4-х
х²-5х+4=0
х1+х2=5 и х1*х2=4
х1=1 и х2=4
Фигура ограничена сверху параболой,а снизу прямой
Автор ответа:
0
Считаем площадь фигуры между двумя графиками по формуле
 ,
,
где f(x)- кривая, график, которой расположен выше кривой у=g(x);
a и b - абсциссы точек пересечения графиков; a<b.
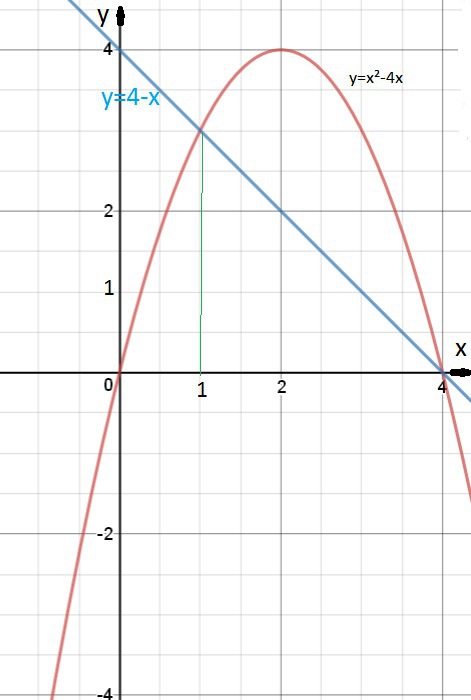
Строим графики функций ( см. рис. в приложении):
у=4х-х²- парабола, ветви которой направлены вверх, точки пересечения с осью Ох:
х=0; х=4
Координаты вершины (2;4).
у=4-х - прямая, проходящая через точки (0;4) и (4;0).
Находим абсциссы точек пересечения графиков функций:
4х-х²=4-х;
х²-5х+4=0
D=25-4·4=9
x=(5-3)/2=1 или х=(5+3)/2=4


кв. ед.
О т в е т. S=4,5 кв. ед.
где f(x)- кривая, график, которой расположен выше кривой у=g(x);
a и b - абсциссы точек пересечения графиков; a<b.
Строим графики функций ( см. рис. в приложении):
у=4х-х²- парабола, ветви которой направлены вверх, точки пересечения с осью Ох:
х=0; х=4
Координаты вершины (2;4).
у=4-х - прямая, проходящая через точки (0;4) и (4;0).
Находим абсциссы точек пересечения графиков функций:
4х-х²=4-х;
х²-5х+4=0
D=25-4·4=9
x=(5-3)/2=1 или х=(5+3)/2=4
кв. ед.
О т в е т. S=4,5 кв. ед.
Приложения:
Похожие вопросы
Предмет: Математика,
автор: СладкаяДевочка3
Предмет: Английский язык,
автор: krasukovadana31
Предмет: Математика,
автор: morvak38
Предмет: Алгебра,
автор: SunKissed