Основание пирамиды-это только боковой треугольник со сторонами 15, 15 и 20 см. Высота пирамиды равна 12 см. Найдите объем перамиды.
Ответы
Ответ:
Объем пирамиды можно найти по формуле:
V = (1/3) * S * h,где S - площадь основания, h - высота пирамиды.
Для начала нужно найти площадь боковой поверхности пирамиды, которая является равнобедренным треугольником. Для этого найдём его высоту через теорему Пифагора:
a^2 + (h')^2 = b^2,где a и b - катеты треугольника, h' - его высота.
Так как треугольник равнобедренный, то a = 15/2 = 7.5 см. Также, так как боковые грани треугольной пирамиды равнобедренные, то b = 20 см. Тогда можно найти высоту боковой грани:
h' = sqrt(b^2 - a^2) = sqrt(20^2 - 7.5^2) = 18.7 см.
Площадь основания пирамиды равна площади треугольника:
S = (1/2) * a * b = (1/2) * 15/2 * 20 = 75 см^2.
Теперь можно найти объем пирамиды:
V = (1/3) * S * h = (1/3) * 75 * 12 = 300 см^3.
Ответ: объем пирамиды равен 300 кубическим сантиметрам.
Объяснение:
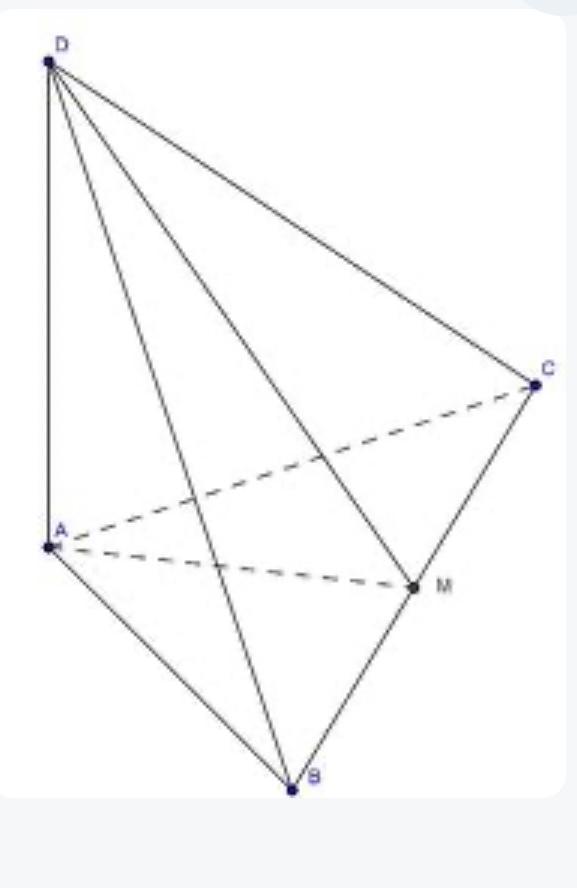
Ответ:1)Построим данное сечение:строим АМ перпендикуляр к гипотенузе ВС, тогда ДМ перпендикуляр к ВС (теорема о 3-х перпендикулярах).ДМ -наклонная, ДА-перпендикуляр к пл-ти АВС, АМ-проекция наклонной, тогда ВС перпендикулярна и к ДМ, след-но ВС пер-на плоскости(АДМ).2) Площади тр-ка АДМ-прям. равна S= 0,5*АД* АМ. ! АД=16 см , АМ-?3) Из тр-ка АВС-прям.: ВС=25 см, т.к. данный тр-к подобен " египетскому" (!!! 3,4,5) с коэфф.5. Площадь АВС равна: S1= 0,5*АВ*АС=0,5*20*15=150 (см^2). С др. стороны S1= 0,5*ВС*АМ=150 0,5* 25*АМ =150 АМ =12.4)S = 0,5*АД* АМ= = 0,5*16* 12= 96 (cм^2). Ответ: 96 cм^2.
Объяснение: