знайти суму та різницю дробів: а) x+y/a-3+x-y/a-3, б) x^2/x-y+y^2/y-x, в) n/abm+m/abn г)x-y/x+y+y^2/2xy+y^2+x^2, д) x+n/x^3-n^3-1/x^2+xn+n^2
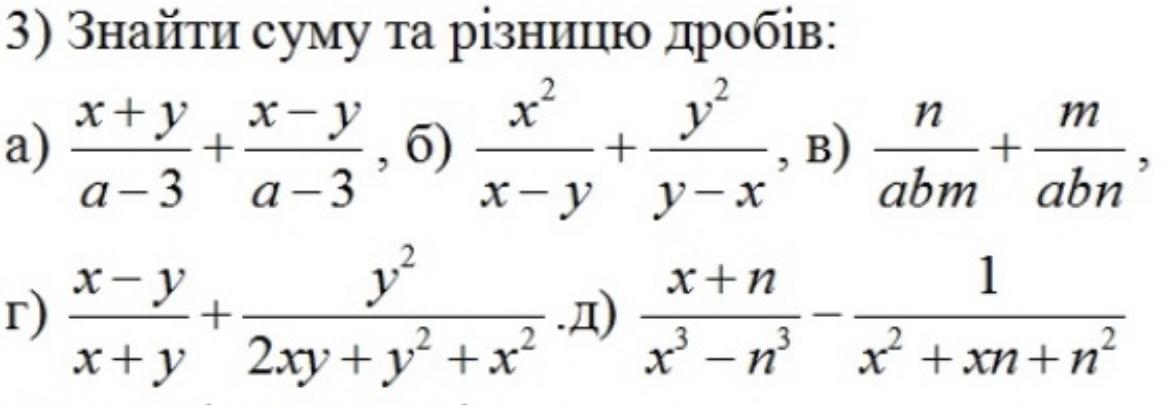
Ответы
Ответ и Объяснение:
Требуется найти сумму и разницу дробей.
Информация. 1) Основное свойство дроби. Если числитель и знаменатель дроби умножить или разделить на одно и то же ненулевое число, то получится равная ей дробь.
2) При сложении или вычитании дробей с одинаковыми знаменателями складываем или вычитаем числители.
Чтобы найти сумму или разность двух дробей с разными знаменателями, нужно сначала привести их к общему знаменателю, а затем воспользоваться правилом сложения или вычитания дробей с одинаковыми знаменателями.
3) Формулы сокращённого умножения.
a) a²-b² = (a-b)·(a+b).
b) a³-b³ = (a-b)·(a²-a·b+b²).
c) (a+b)² = a²+2·a·b+b².
Решение. При вычислении применим нужные из вышеприведённых свойств или способов.
а) Знаменатели дробей равны:
б) Знаменатели дробей отличаются знаком:
в) Знаменатели дробей разные, применим основное свойство дробей:
г) Знаменатели дробей разные, преобразуем и применим основное свойство дробей:
д) Знаменатели дробей разные, преобразуем и применим основное свойство дробей:
#SPJ1