Предмет: Алгебра,
автор: aqw50
ПОМОГИТЕ ПОЖАЛУЙСТА 60!!!!!!!!!!!!!!
Приложения:
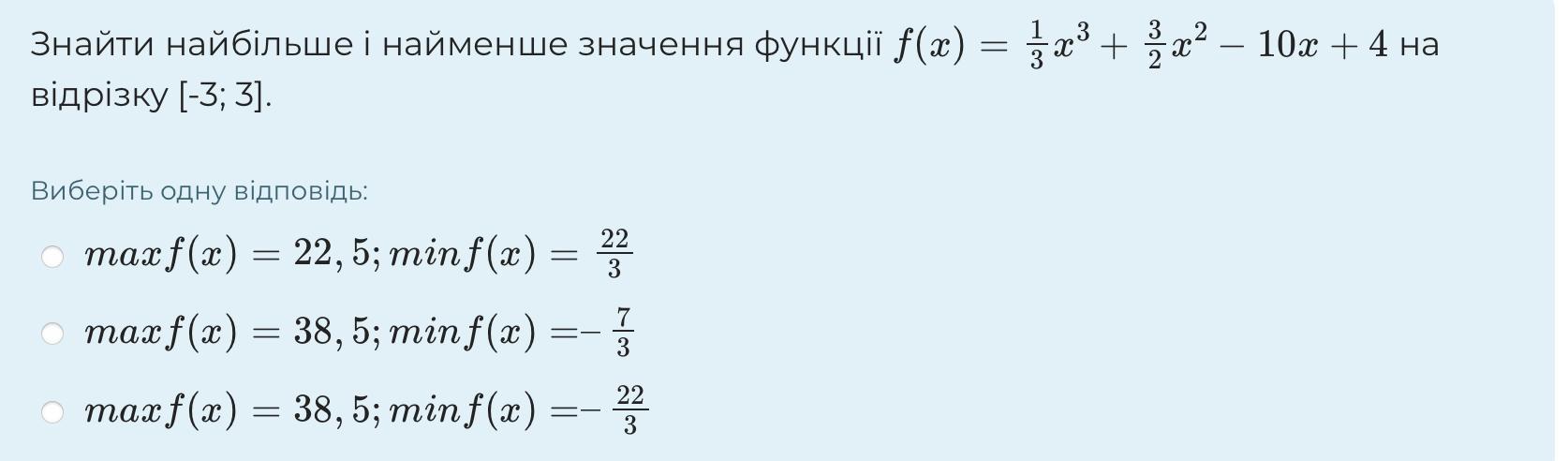
Ответы
Автор ответа:
0
Ответ:
maxf(x)=38.5
minf(x)=
Объяснение:
Для нахождения наибольшего и наименьшего значения функции найдем ее производную и прировняем ее к нулю:
⇒(x+5)(x-2)⇒
точка 2∈[-3;3] поэтому ее берем и крайние точки данного отрезка.
теперь среди найденных значений осталось выбрать наибольшее и наименьшее значения.
Похожие вопросы
Предмет: Немецкий язык,
автор: ichvilnicht
Предмет: Окружающий мир,
автор: komisarenkovika838
Предмет: География,
автор: anastasiaresetnak467
Предмет: География,
автор: gylnara2104