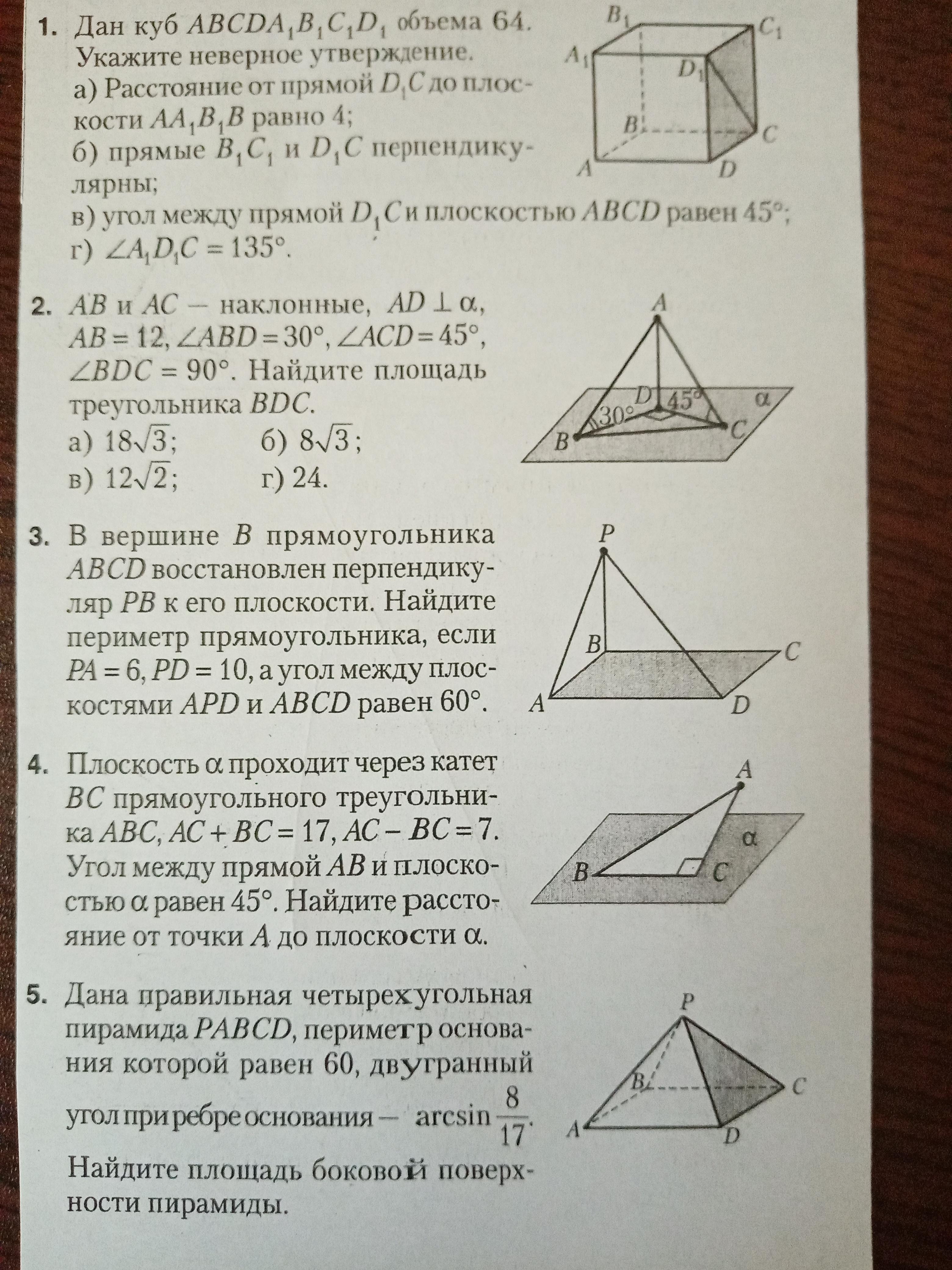
2)AB и AC - наклонные, AD перпендикулярно альфа, АВ=12, АВD=30°, ACD=45°, BDC=90°.
И можно ещё 5 задачу
Ответы
Ответ:
Сначала найдем AD, используя тригонометрию треугольника ABD:
ABD = 30°, AB = 12
cos(30°) = AD/AB
AD = 12*cos(30°) = 10.3923
Затем найдем CD, используя тригонометрию треугольника ACD:
ACD = 45°, AC = AD/cos(ACD)
AC = 10.3923/cos(45°) = 14.697
Теперь найдем BD, используя теорему Пифагора в треугольнике BDC:
BD^2 = BC^2 + CD^2
BD^2 = AB^2 - AC^2 + CD^2
BD^2 = 12^2 - 14.697^2 + CD^2
BD^2 = 39.999 - 215.771 + CD^2
BD^2 = -175.772 + CD^2
Так как BDC - прямоугольный треугольник, то BD - гипотенуза, а CD и BC - катеты. Из этого следует, что BD > CD. Однако мы видим, что выражение под корнем отрицательно, значит, такой треугольник не может существовать. Значит, что-то было неверно в изначальных данных.
5)
Поскольку периметр основания равен 60, то каждая сторона основания должна быть равна 15 (60/4). Обозначим точку пересечения диагоналей основания как O.
Так как угол при ребре основания равен arcsin(8/17), можно найти значение косинуса этого угла как sin(90° - arcsin(8/17)):
cos(arcsin(8/17)) = sin(90° - arcsin(8/17)) = 15/17
Теперь можем найти высоту пирамиды по теореме Пифагора в треугольнике AOB (где AB=15, BO=OA=h):
h^2 = AB^2 - AO^2
h^2 = 15^2 - (15/2)^2
h^2 = 450 - 112.5
h^2 = 337.5
h = √(337.5)
Теперь можно найти площадь боковой поверхности пирамиды (Sб) как сумму площадей боковых граней:
Sб = SABC + SABD + SACD
Так как основание правильной пирамиды - квадрат, то треугольники ABC и ABD равнобедренные со сторонами AB=15 и AC=AD=BD=2h/√2 (по свойствам правильной пирамиды). Тогда площадь каждого из этих треугольников будет равна:
SABC = SABD = 1/2 * AC * AB = 1/2 * 15 * 2h/√2 = 15h/√2
Треугольник ACD - прямоугольный с гипотенузой AC=2h. Тогда его площадь равна:
SACD = 1/2 * AC * CD = 1/2 * 2h * h = h^2
Теперь можно подставить найденные значения и посчитать площадь боковой поверхности:
Sб = SABC + SABD + SACD = 15h/√2 + 15h/√2 + h^2 = 30h/√2 + h^2
Заметим, что h^2 = 337.5, а √2 ≈ 1.414. Тогда:
Sб = 30h/√2 + h^2 ≈ 30 * 18.97 + 337.5 ≈ 877.1
Ответ: площадь боковой поверхности пирамиды примерно равна 877.1.
Объяснение:
пон ._.