(x+4)*(x-2)-(4x-3)*(x+5)=x*(x-3) помогите срочно
Ответы
Ответ:вот
Объяснение:

Відповідь:Розглянемо рівняння:
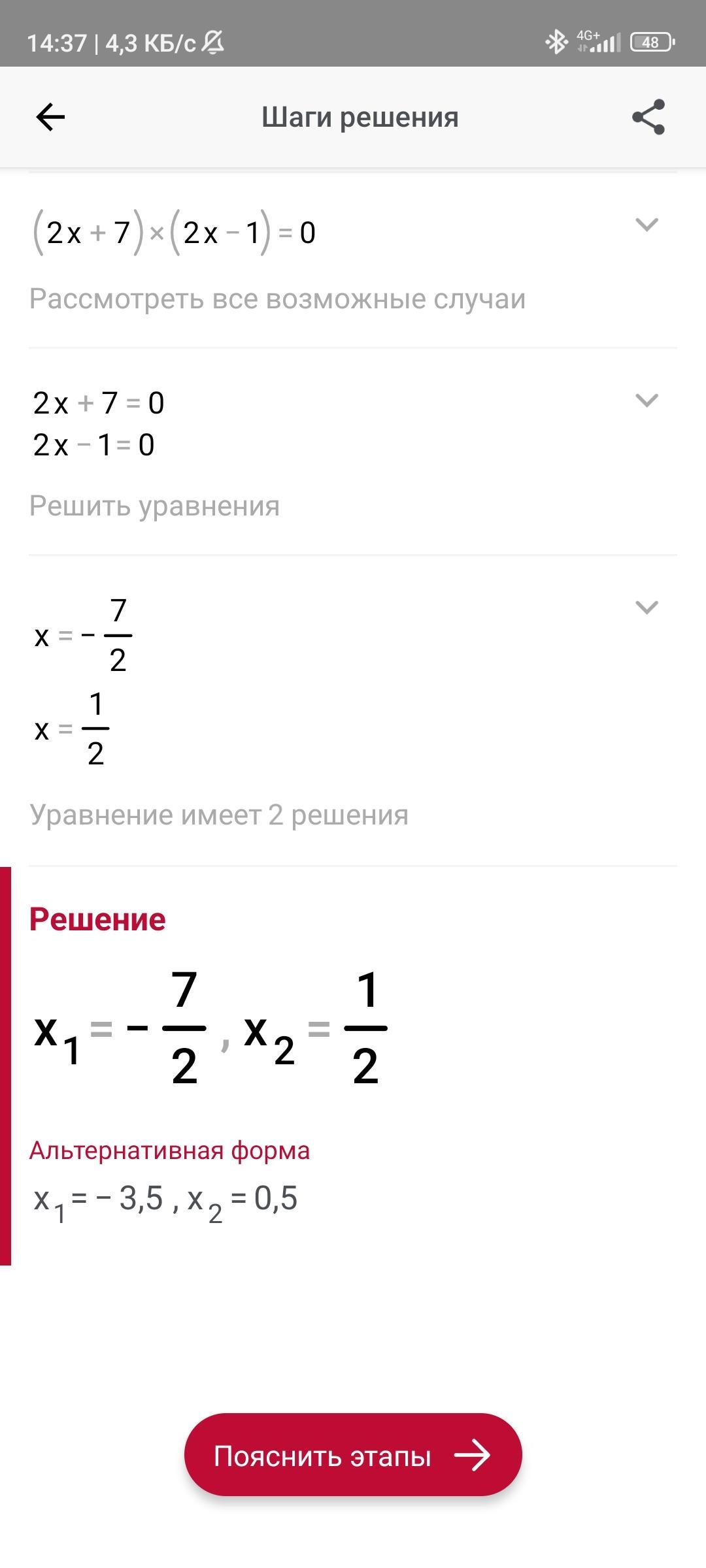
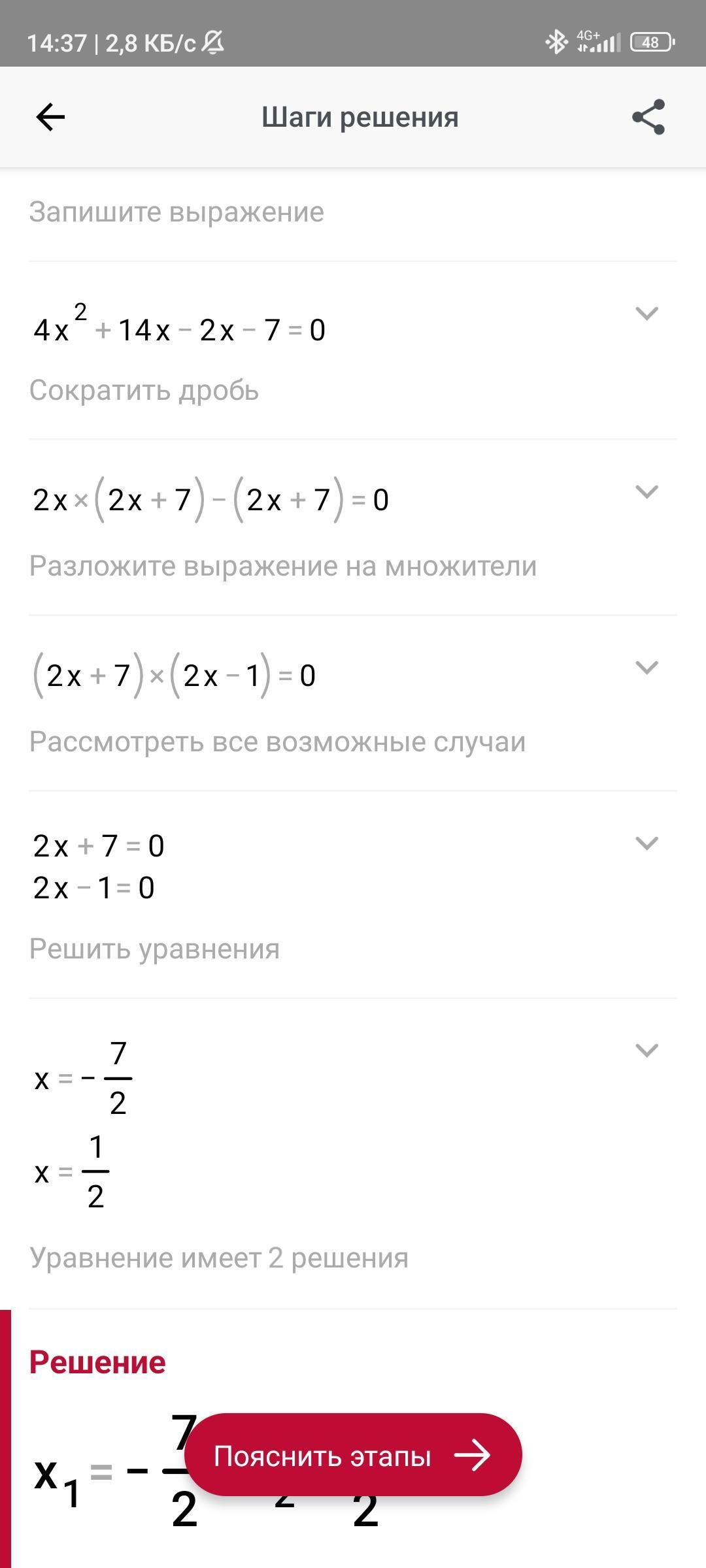
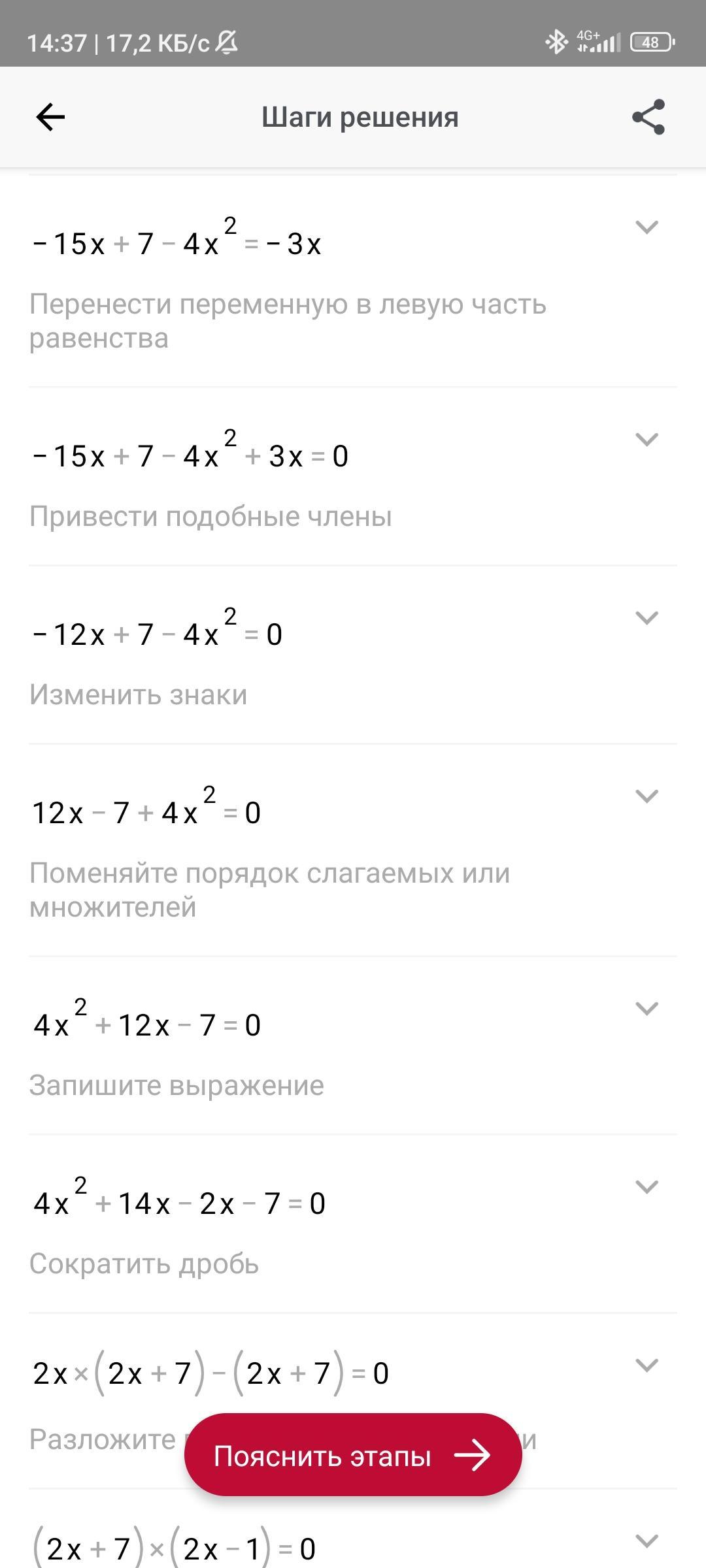
(x+4)(x-2)-(4x-3)(x+5)=x*(x-3)
Спочатку розкриваємо дужки за допомогою формули різниці квадратів:
(x^2+4x-8)-(4x^2+17x-15)=x^2-3x
Потім скорочуємо подібні члени на лівій та правій стороні рівняння:
x^2+4x-8-4x^2-17x+15=x^2-3x
Після цього переносимо всі члени на одну сторону та скорочуємо подібні:
-3x^2-9x+23=0
Розв'язуємо квадратне рівняння за допомогою формули коренів:
x = (-(-9) ± √((-9)^2 - 4*(-3)23)) / (2(-3))
x = (9 ± √(249)) / (-6)
Отже, ми отримали два розв'язки:
x ≈ -3.09 або x ≈ 2.42
Перевіримо, що обидва значення задовольняють початкове рівняння:
для x ≈ -3.09:
(x+4)(x-2)-(4x-3)(x+5)=(-3.09+4)(-3.09-2)-(4(-3.09)-3)(-3.09+5) ≈ -9.81
x(x-3)=(-3.09)*(-3.09-3) ≈ -12.48
Отже, x ≈ -3.09 не є розв'язком.
для x ≈ 2.42:
(x+4)(x-2)-(4x-3)(x+5)=(2.42+4)(2.42-2)-(42.42-3)(2.42+5) ≈ -0.02
x(x-3)=(2.42)*(2.42-3) ≈ -0.60
Отже, x ≈ 2.42 є розв'язком рівняння.
Отже, єдиний розв'язок рівняння: x ≈ 2.42.
Пояснення:Ось так)