Question

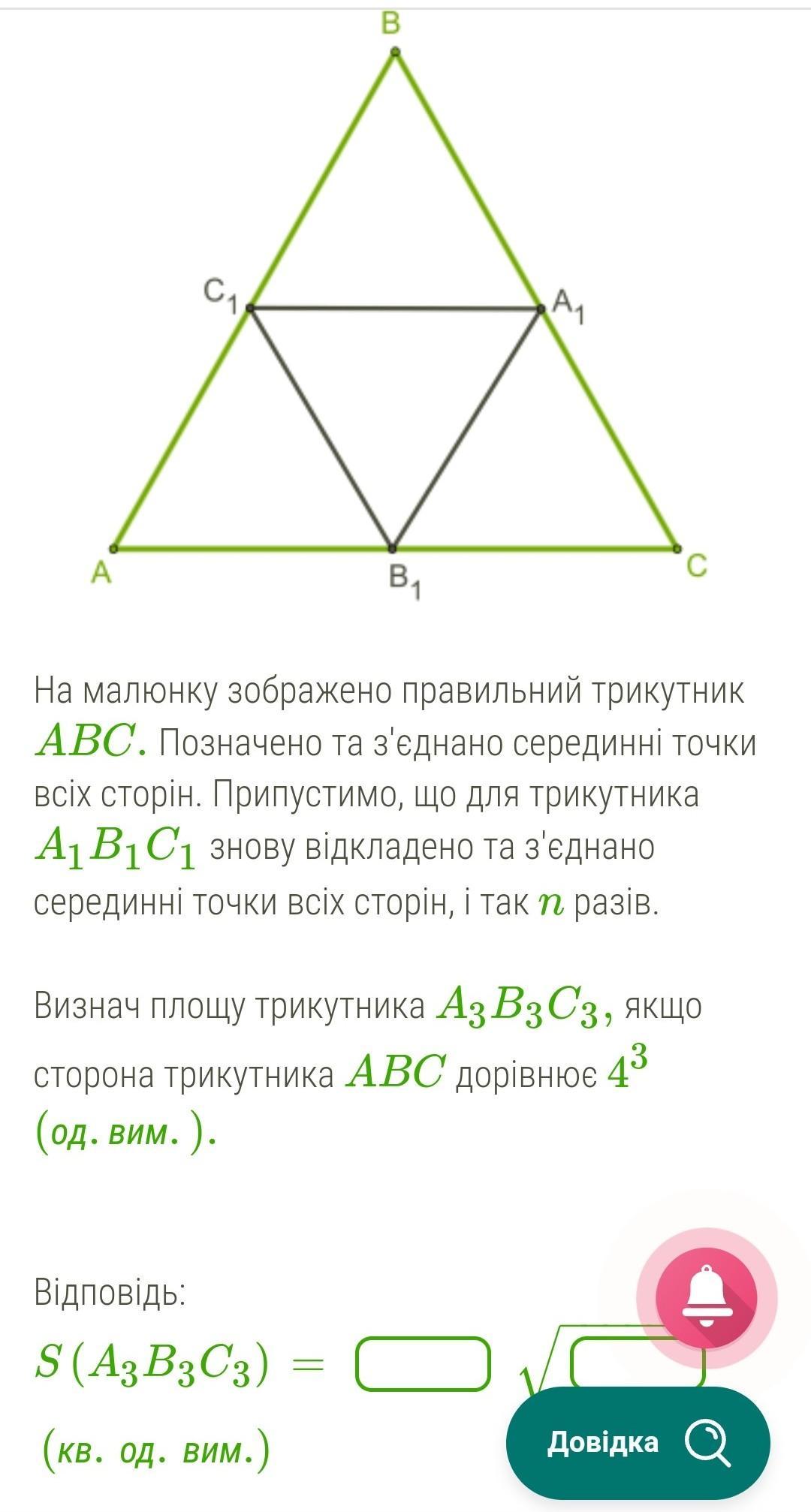
На малюнку зображено правильний трикутник ABC. Позначено та з'єднано серединні точки всіх сторін. Припустимо, що для трикутника A1B1C1 знову відкладено та з'єднано серединні точки всіх сторін, і так n разів. Визнач площу трикутника A3B3C3, якщо сторона трикутника ABC дорівнює 43 (од.вим.). Відповідь: S(A3B3C3)= −−−−−−−√(кв.од.вим.).

прошу, допоможіть.. дам 50 балів. будь ласка,з поясненням ​

Answer 1

Відповідь:

треугольников АВС и А1В1С1:

Оба они правильные(углы равны по 60°) => они подобные.

2) Найдем коэффициент подобия:

А1С1 = 1/2АС(так как А1С1 - средняя линия); аналогично все стороны маленького треугольника меньше чем стороны большого треугольника в 2 раза => k = 1/2

Значит k^2 = Sавс/Sa1b1c1 = 1/4;

I - способ

3)Можно решить многими способами, но я выберу геометрическую прогрессию:

S = 45; q = 1/4; S5 - ?

S5 = 45 * (1/4)^5 = 45 * 1/1024= 0.044 единиц квадратных

II - способ

Площадь любого правильно треугольника можна посчитать по формуле S = a^2√3/4

Sabc = a^2√3/4 = 45;

a^2 = 180/√3

Sa1b1c1 = (a^2 / 1024 * √3 / 4 ) = 45/1024 = 0,044

................................................................................................