Предмет: Алгебра,
автор: kotlkaty17
Допоможіть, будь ласка!
Приложения:
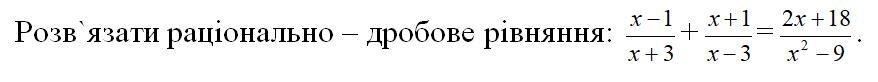
Ответы
Автор ответа:
2
Автор ответа:
1
Ответ:
- по формуле сокращённого умножения преобразовал x²-9
- перенёс дробь из правой части в левую
- фонтанчиком раскрыл скобки
- сложил все числа
- в числителе получил квадратное уравнение, а в знаменателе две скобки, ни одна из которых не должна равняться 0 т.к. знаменатель не равен 0 (это записано в ОДЗ)
- ОДЗ- область допустимых значений. нашёл чему неравен X
- решил квадратное уравнение, которое было в чимлителе и нашёл то что один из корней равняется 3, который не должен равняться 3 (по ОДЗ)
- записал в ответ один корень, который является решением этого уравнения
Приложения:

Похожие вопросы
Предмет: Математика,
автор: amusazade2013
Предмет: Химия,
автор: komendrayuliya
Предмет: Українська мова,
автор: HEKTO23
Предмет: Алгебра,
автор: vegcnns58
Предмет: Английский язык,
автор: Li19za