Предмет: Алгебра,
автор: uyvgfyudfukgf765877v
АЛГЕБРАААААА!!!!!!!!!!!!!!!!!!!!!!!!!!!!1
Приложения:
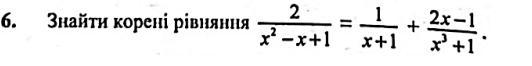
Ответы
Автор ответа:
0
Ответ: x=2.
Объяснение:
ОДЗ:
Решение:
Похожие вопросы
Предмет: Химия,
автор: iblks591
Предмет: Математика,
автор: Аноним
Предмет: Математика,
автор: polinanovokresennaa
Предмет: Химия,
автор: Pobin05