Question

Ответ с объяснением обязательно ​

Answer 1

Ответ:

8.

Пошаговое объяснение:

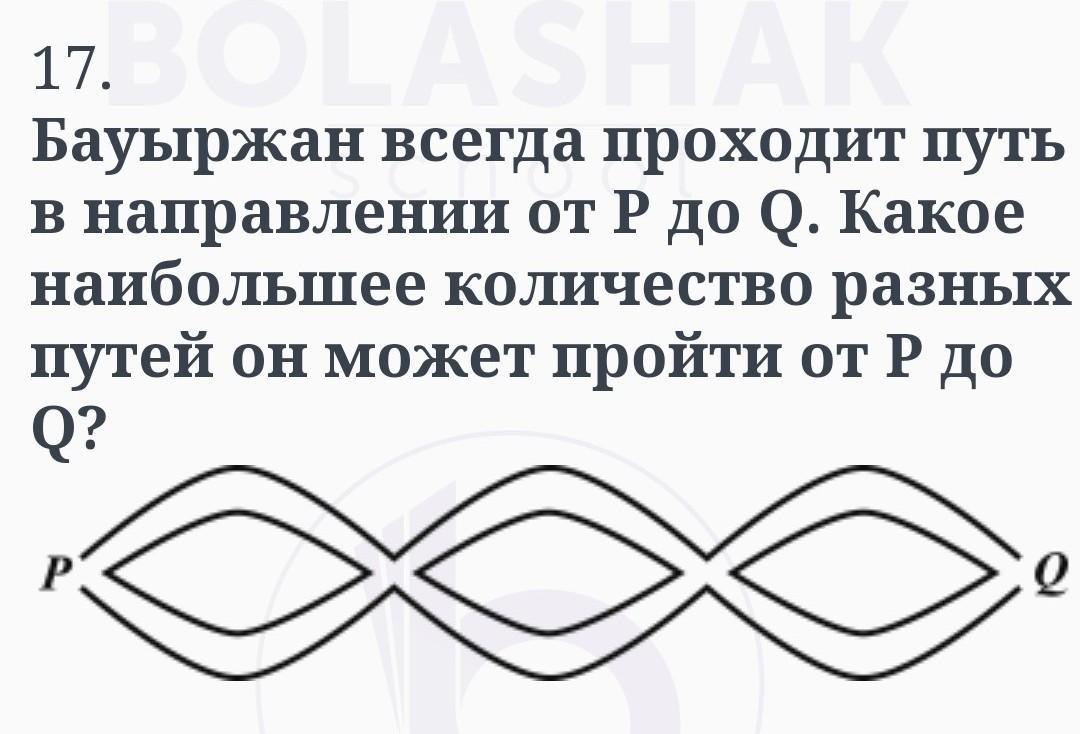
Когда Бауыржан выходит из пункта P, у него две возможности - пойти или левой тропинкой или правой. Какой путь он ни выберет, он обязательно дойдет до первой точки пересечения тропинок. В этот момент у него опять будут две возможности - пойти налево или направо. Аналогичная ситуация возникнет в момент, когда он достигнет второго пересечения тропинок - снова он может пойти налево или направо. Поэтому всего у него 2·2·2=8 различных способов пройти от P к Q.

Если моё рассуждение не кажется очевидным, можно рассуждать так. Будем задавать каждый способ перемещения от P к Q  последовательностью букв Л (налево) и П (направо). Скажем, если он каждый раз будет выбирать левую тропинку, мы напишем ЛЛЛ, если, скажем, сначала он пойдет левой тропинкой, а затем дважды правой, мы напишем ЛПП, и так далее.

Тогда мы имеем следующие возможности движения:

ЛЛЛ, ЛЛП, ЛПЛ, ЛПП, ПЛЛ, ПЛП, ППЛ, ППП - всего 8 способов.

Кстати, мне больше нравится вместо букв Л и П писать цифры, а именно 0 и 1. Тогда мы будем иметь следующие возможности:

000, 001, 010, 011, 100, 101, 110, 111.