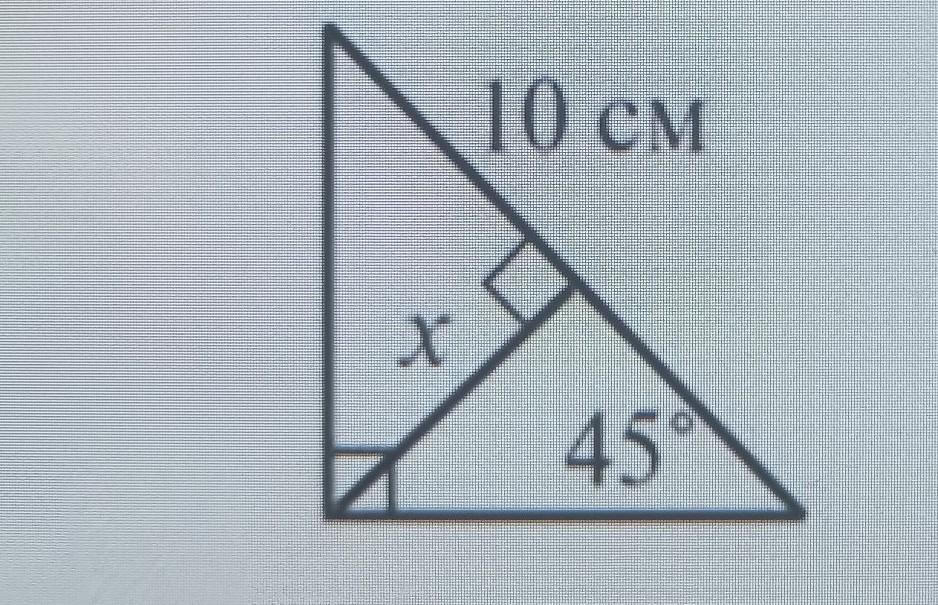
Срочно даю 50 Знайдіть висоту прямокутного трикутника, яка проведена до гіпотенузи.
Ответы
Пусть прямоугольный треугольник имеет катеты a и b, а гипотенуза c. Тогда в соответствии с теоремой Пифагора c^2 = a^2 + b^2.
Пусть h - высота, опущенная на гипотенузу c.
Тогда мы можем выразить площадь треугольника двумя способами:
S = (a * h)/2 и S = (b * h)/2
Сравнивая эти выражения, получаем:
(a * h)/2 = (b * h)/2
h/2 * (a - b) = 0
Так как a и b положительны (они являются длинами сторон), то a - b ≠ 0, откуда следует, что h = 0 не может быть решением.
Таким образом, мы можем сократить h/2 из обеих частей уравнения и получить:
a = b
То есть, если прямоугольный треугольник равнобедренный, то высота, проведенная к гипотенузе, является его медианой и равна половине гипотенузы.
Если треугольник не равнобедренный, то нужно использовать формулу для нахождения высоты:
h = (a * b) / c, где c - гипотенуза.
Таким образом, чтобы найти высоту прямоугольного треугольника, нужно знать длины его катетов и гипотенузы, и если треугольник не равнобедренный, использовать формулу h = (a * b) / c.