Предмет: Алгебра,
автор: Ангелина12398
1) известно что:
2) упростите выражения
3) докажите тождество
Приложения:
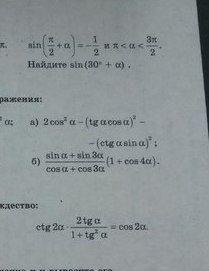
Ответы
Автор ответа:
0
Автор ответа:
0
1)
![sin(frac{pi}{2}+alpha)=-frac{1}{2}; \
pi<alpha<frac{3pi}{2}; alphain(pi;frac{2pi}{3});\
sin(30^0+alpha)-?;\
frac{pi}{2}+alpha=(-1)^narcsin(-frac{1}{2})+pi n; nin Z\
alpha=-(-1)^narcsin(frac{1}{2})-frac{pi}{2}+pi n;\
alpha=(-1)^{n+1}cdotfrac{pi}{6}-frac{pi}{2}+pi n;\
n=2: alpha=-frac{pi}{6}-frac{pi}{2}+2pi=frac{-pi-3pi+12pi}{6}=frac{8pi}{6}=frac{4pi}{3}in(pi;frac{2pi}{3});\](https://tex.z-dn.net/?f=sin%28frac%7Bpi%7D%7B2%7D%2Balpha%29%3D-frac%7B1%7D%7B2%7D%3B++%5C%0Api%26lt%3Balpha%26lt%3Bfrac%7B3pi%7D%7B2%7D%3B+alphain%28pi%3Bfrac%7B2pi%7D%7B3%7D%29%3B%5C%0Asin%2830%5E0%2Balpha%29-%3F%3B%5C%0Afrac%7Bpi%7D%7B2%7D%2Balpha%3D%28-1%29%5Enarcsin%28-frac%7B1%7D%7B2%7D%29%2Bpi+n%3B+nin+Z%5C%0Aalpha%3D-%28-1%29%5Enarcsin%28frac%7B1%7D%7B2%7D%29-frac%7Bpi%7D%7B2%7D%2Bpi+n%3B%5C%0Aalpha%3D%28-1%29%5E%7Bn%2B1%7Dcdotfrac%7Bpi%7D%7B6%7D-frac%7Bpi%7D%7B2%7D%2Bpi+n%3B%5C%0An%3D2%3A++alpha%3D-frac%7Bpi%7D%7B6%7D-frac%7Bpi%7D%7B2%7D%2B2pi%3Dfrac%7B-pi-3pi%2B12pi%7D%7B6%7D%3Dfrac%7B8pi%7D%7B6%7D%3Dfrac%7B4pi%7D%7B3%7Din%28pi%3Bfrac%7B2pi%7D%7B3%7D%29%3B%5C "sin(frac{pi}{2}+alpha)=-frac{1}{2}; \
pi<alpha<frac{3pi}{2}; alphain(pi;frac{2pi}{3});\
sin(30^0+alpha)-?;\
frac{pi}{2}+alpha=(-1)^narcsin(-frac{1}{2})+pi n; nin Z\
alpha=-(-1)^narcsin(frac{1}{2})-frac{pi}{2}+pi n;\
alpha=(-1)^{n+1}cdotfrac{pi}{6}-frac{pi}{2}+pi n;\
n=2: alpha=-frac{pi}{6}-frac{pi}{2}+2pi=frac{-pi-3pi+12pi}{6}=frac{8pi}{6}=frac{4pi}{3}in(pi;frac{2pi}{3});\")
![sin(30^0+alpha)=sin(frac{pi}{6}+frac{4pi}{3})=sin(frac{pi+8pi}{6})=\
=sinfrac{9pi}{6}=sin{frac{3pi}{2}}-1;\
or: sinfrac{pi}{6}cosfrac{4pi}{3}+sin{frac{4pi}{3}}cosfrac{pi}{6}=\
=frac{1}{2}cdot(-frac{1}{2})+(-frac{sqrt{3}}{2})cdotfrac{sqrt{3}}{2}=-frac{1}{4}-frac{3}{4}=-frac{4}{4}=-1](https://tex.z-dn.net/?f=sin%2830%5E0%2Balpha%29%3Dsin%28frac%7Bpi%7D%7B6%7D%2Bfrac%7B4pi%7D%7B3%7D%29%3Dsin%28frac%7Bpi%2B8pi%7D%7B6%7D%29%3D%5C%0A%3Dsinfrac%7B9pi%7D%7B6%7D%3Dsin%7Bfrac%7B3pi%7D%7B2%7D%7D-1%3B%5C%0Aor%3A+sinfrac%7Bpi%7D%7B6%7Dcosfrac%7B4pi%7D%7B3%7D%2Bsin%7Bfrac%7B4pi%7D%7B3%7D%7Dcosfrac%7Bpi%7D%7B6%7D%3D%5C%0A%3Dfrac%7B1%7D%7B2%7Dcdot%28-frac%7B1%7D%7B2%7D%29%2B%28-frac%7Bsqrt%7B3%7D%7D%7B2%7D%29cdotfrac%7Bsqrt%7B3%7D%7D%7B2%7D%3D-frac%7B1%7D%7B4%7D-frac%7B3%7D%7B4%7D%3D-frac%7B4%7D%7B4%7D%3D-1 "sin(30^0+alpha)=sin(frac{pi}{6}+frac{4pi}{3})=sin(frac{pi+8pi}{6})=\
=sinfrac{9pi}{6}=sin{frac{3pi}{2}}-1;\
or: sinfrac{pi}{6}cosfrac{4pi}{3}+sin{frac{4pi}{3}}cosfrac{pi}{6}=\
=frac{1}{2}cdot(-frac{1}{2})+(-frac{sqrt{3}}{2})cdotfrac{sqrt{3}}{2}=-frac{1}{4}-frac{3}{4}=-frac{4}{4}=-1")
![sin(30^0+alpha)=-1;\](https://tex.z-dn.net/?f=sin%2830%5E0%2Balpha%29%3D-1%3B%5C "sin(30^0+alpha)=-1;\")
2)
a)
![2cos^2alpha-(tgalphacdotcosalpha)^2-(ctgalphacdotsinalpha)^2=\
=2cos^2alpha-left(left(frac{sinalpha}{cosalpha}cdotcosalpharight)^2+left(frac{cosalpha}{sinalpha}cdot sinalpharight)^2right)=\
=2cos^2alpha-left(sin^2alpha+cos^2alpharight)=2cos^2alpha-1=cos2alpha;\](https://tex.z-dn.net/?f=2cos%5E2alpha-%28tgalphacdotcosalpha%29%5E2-%28ctgalphacdotsinalpha%29%5E2%3D%5C%0A%3D2cos%5E2alpha-left%28left%28frac%7Bsinalpha%7D%7Bcosalpha%7Dcdotcosalpharight%29%5E2%2Bleft%28frac%7Bcosalpha%7D%7Bsinalpha%7Dcdot+sinalpharight%29%5E2right%29%3D%5C%0A%3D2cos%5E2alpha-left%28sin%5E2alpha%2Bcos%5E2alpharight%29%3D2cos%5E2alpha-1%3Dcos2alpha%3B%5C%0A "2cos^2alpha-(tgalphacdotcosalpha)^2-(ctgalphacdotsinalpha)^2=\
=2cos^2alpha-left(left(frac{sinalpha}{cosalpha}cdotcosalpharight)^2+left(frac{cosalpha}{sinalpha}cdot sinalpharight)^2right)=\
=2cos^2alpha-left(sin^2alpha+cos^2alpharight)=2cos^2alpha-1=cos2alpha;\")
б)
![frac{sinalpha+sin3alpha}{cosalpha+cos3alpha}cdot(1+cos4alpha)=\
=frac{sinalpha+sin(alpha+2alpha)}{cosalpha+cos(alpha+2alpha)}cdot(1+2cos^22alpha-1)=\
=frac{sinalpha+sinalphacos2alpha+cosalphasin2alpha}{cosalpha+cosalphacos2alpha-sinalphasin2alpha}cdot2cos^22alpha=\
==frac{sinalpha+sinalphacos2alpha+2cos^2alphasinalpha}{cosalpha+cosalphacos2alpha-2sin^2alphacosalpha}cdot2cos^22alpha=\](https://tex.z-dn.net/?f=frac%7Bsinalpha%2Bsin3alpha%7D%7Bcosalpha%2Bcos3alpha%7Dcdot%281%2Bcos4alpha%29%3D%5C%0A%3Dfrac%7Bsinalpha%2Bsin%28alpha%2B2alpha%29%7D%7Bcosalpha%2Bcos%28alpha%2B2alpha%29%7Dcdot%281%2B2cos%5E22alpha-1%29%3D%5C%0A%3Dfrac%7Bsinalpha%2Bsinalphacos2alpha%2Bcosalphasin2alpha%7D%7Bcosalpha%2Bcosalphacos2alpha-sinalphasin2alpha%7Dcdot2cos%5E22alpha%3D%5C%0A%3D%3Dfrac%7Bsinalpha%2Bsinalphacos2alpha%2B2cos%5E2alphasinalpha%7D%7Bcosalpha%2Bcosalphacos2alpha-2sin%5E2alphacosalpha%7Dcdot2cos%5E22alpha%3D%5C "frac{sinalpha+sin3alpha}{cosalpha+cos3alpha}cdot(1+cos4alpha)=\
=frac{sinalpha+sin(alpha+2alpha)}{cosalpha+cos(alpha+2alpha)}cdot(1+2cos^22alpha-1)=\
=frac{sinalpha+sinalphacos2alpha+cosalphasin2alpha}{cosalpha+cosalphacos2alpha-sinalphasin2alpha}cdot2cos^22alpha=\
==frac{sinalpha+sinalphacos2alpha+2cos^2alphasinalpha}{cosalpha+cosalphacos2alpha-2sin^2alphacosalpha}cdot2cos^22alpha=\")
![=frac{sinalpha(1+cos2alpha+2cos^2alpha)}{cosalpha(1+cos2alpha-2sin^2alpha)}cdot2cos^22alpha=\
frac{sinalpha(1+2cos^2alpha-1+2cos^2alpha)}{cosalpha(cos2alpha+1-2sin^2alpha)}cdot2cos^22alpha=\
=frac{sinalphacdot4cos^2alpha}{cosalphacdot2cos2alpha}cdot2cos^22alpha=\
=4sinalphacosalphacos2alpha=2sin2alpha2cos2alpha=sin4alpha;\](https://tex.z-dn.net/?f=%3Dfrac%7Bsinalpha%281%2Bcos2alpha%2B2cos%5E2alpha%29%7D%7Bcosalpha%281%2Bcos2alpha-2sin%5E2alpha%29%7Dcdot2cos%5E22alpha%3D%5C%0Afrac%7Bsinalpha%281%2B2cos%5E2alpha-1%2B2cos%5E2alpha%29%7D%7Bcosalpha%28cos2alpha%2B1-2sin%5E2alpha%29%7Dcdot2cos%5E22alpha%3D%5C%0A%3Dfrac%7Bsinalphacdot4cos%5E2alpha%7D%7Bcosalphacdot2cos2alpha%7Dcdot2cos%5E22alpha%3D%5C%0A%3D4sinalphacosalphacos2alpha%3D2sin2alpha2cos2alpha%3Dsin4alpha%3B%5C "=frac{sinalpha(1+cos2alpha+2cos^2alpha)}{cosalpha(1+cos2alpha-2sin^2alpha)}cdot2cos^22alpha=\
frac{sinalpha(1+2cos^2alpha-1+2cos^2alpha)}{cosalpha(cos2alpha+1-2sin^2alpha)}cdot2cos^22alpha=\
=frac{sinalphacdot4cos^2alpha}{cosalphacdot2cos2alpha}cdot2cos^22alpha=\
=4sinalphacosalphacos2alpha=2sin2alpha2cos2alpha=sin4alpha;\")
3)
![ctg2alphafrac{2tgalpha}{1+tg^2alpha}=cos2alpha;\
frac{cos2alpha}{sin2alpha}cdotfrac{2frac{sinalpha}{cosalpha}}{1+(frac{sinalpha}{cosalpha})^2}=frac{cos2alpha}{sin2alpha}cdotfrac{2frac{sinalpha}{cosalpha}}{frac{cos^2alpha+sin^2alpha}{cos^2alpha}}=2cdotfrac{cos2alpha}{sin2alpha}cdotfrac{frac{sinalpha}{cosalpha}}{frac{1}{cos^2alpha}}=\
=2cdotfrac{cos2alpha}{sin2alpha}cdotfrac{sinalphacdotcos^2alpha}{cosalpha}=](https://tex.z-dn.net/?f=ctg2alphafrac%7B2tgalpha%7D%7B1%2Btg%5E2alpha%7D%3Dcos2alpha%3B%5C%0Afrac%7Bcos2alpha%7D%7Bsin2alpha%7Dcdotfrac%7B2frac%7Bsinalpha%7D%7Bcosalpha%7D%7D%7B1%2B%28frac%7Bsinalpha%7D%7Bcosalpha%7D%29%5E2%7D%3Dfrac%7Bcos2alpha%7D%7Bsin2alpha%7Dcdotfrac%7B2frac%7Bsinalpha%7D%7Bcosalpha%7D%7D%7Bfrac%7Bcos%5E2alpha%2Bsin%5E2alpha%7D%7Bcos%5E2alpha%7D%7D%3D2cdotfrac%7Bcos2alpha%7D%7Bsin2alpha%7Dcdotfrac%7Bfrac%7Bsinalpha%7D%7Bcosalpha%7D%7D%7Bfrac%7B1%7D%7Bcos%5E2alpha%7D%7D%3D%5C%0A%3D2cdotfrac%7Bcos2alpha%7D%7Bsin2alpha%7Dcdotfrac%7Bsinalphacdotcos%5E2alpha%7D%7Bcosalpha%7D%3D "ctg2alphafrac{2tgalpha}{1+tg^2alpha}=cos2alpha;\
frac{cos2alpha}{sin2alpha}cdotfrac{2frac{sinalpha}{cosalpha}}{1+(frac{sinalpha}{cosalpha})^2}=frac{cos2alpha}{sin2alpha}cdotfrac{2frac{sinalpha}{cosalpha}}{frac{cos^2alpha+sin^2alpha}{cos^2alpha}}=2cdotfrac{cos2alpha}{sin2alpha}cdotfrac{frac{sinalpha}{cosalpha}}{frac{1}{cos^2alpha}}=\
=2cdotfrac{cos2alpha}{sin2alpha}cdotfrac{sinalphacdotcos^2alpha}{cosalpha}=")
2)
a)
б)
3)
Похожие вопросы
Предмет: Русский язык,
автор: yeyehdgd
Предмет: Математика,
автор: rasulevaekaterina
Предмет: Биология,
автор: naidaterikova122
Предмет: Математика,
автор: 32654
Предмет: Математика,
автор: SAMSON57