Предмет: Геометрия,
автор: fucjeit
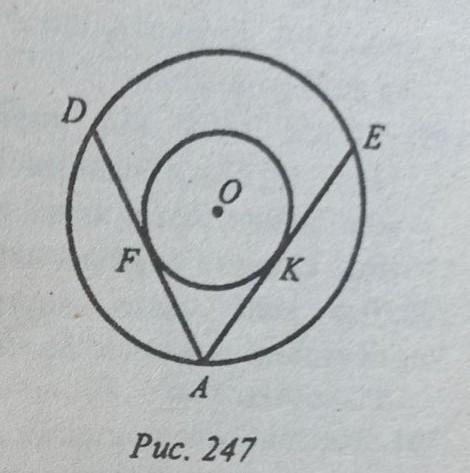
ДАЮ 50 БАЛЛОВ! 193. Два кола мають спільний центр О (рис.247). З точки А кола більшого радіуса проведено дотичнi AF i AK до другого кола, які перетинають перше КОЛО В точках D i E відповідно, ZDAE: 60°, точки F i K - ТОЧКИ дотику. Знайдіть менший з радіусів даних кіл, якщо більший радіус дорів- нює 8 см.
Приложения:
fucjeit:
плииз
Ответы
Автор ответа:
1
Ответ:
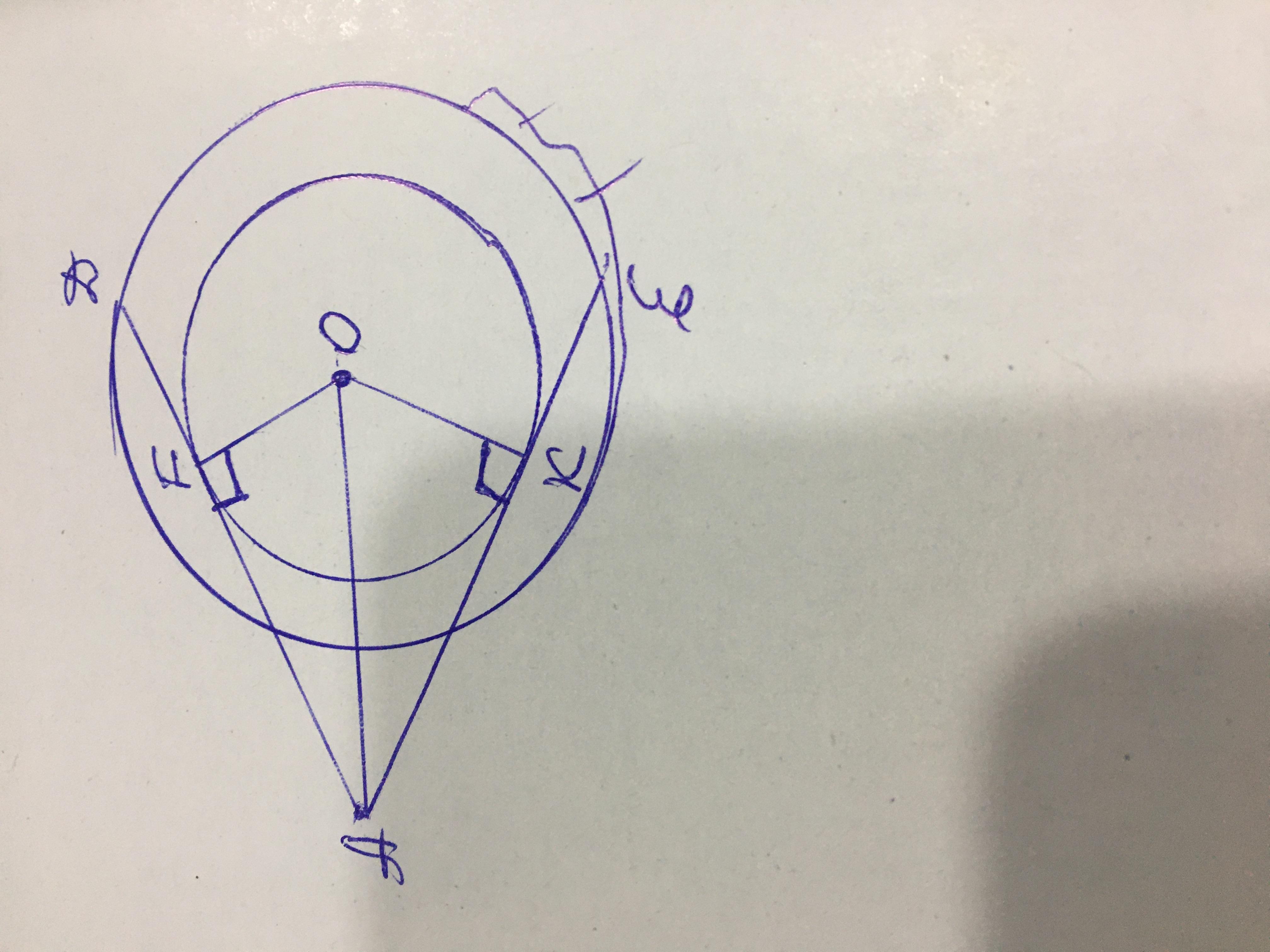
Проведём прямую из точки А до точки О,эта прямая является биссектрисой угла А
<FAO=<KAO=60:2=30 градусов
Соединим точки касания касательных АF и АК с центром окружности радиусами ОF и ОК
Радиусы и касательные перпендикулярны друг другу,радиус ОF перпендикуляр к касательной АF;радиус ОК перпендикуляр к АК,поэтому
<АFO=<AKO=90 градусов
После всех построений у нас образовались два равных прямоугольных треугольника
Рассмотрим один из них
Треугольник АОК прямоугольный
Катет ОК(он же радиус меньшей окружности)лежит напротив угла 30 градусов,а значит-этот катет в два раза меньше гипотенузы АО(она же радиус большой окружности)
ОК=8:2=4 см
Объяснение:
Приложения:
спасибо
Вау!
Супер
Класс)
Похожие вопросы
Предмет: Английский язык,
автор: ernistovanurkyz
Предмет: Математика,
автор: zanabiltaev
Предмет: Алгебра,
автор: vortexplay414
Предмет: Литература,
автор: D1rzyyy
Предмет: Українська література,
автор: wotdanil2020