Предмет: Алгебра,
автор: vortexplay414
доведіть тотожність
Приложения:
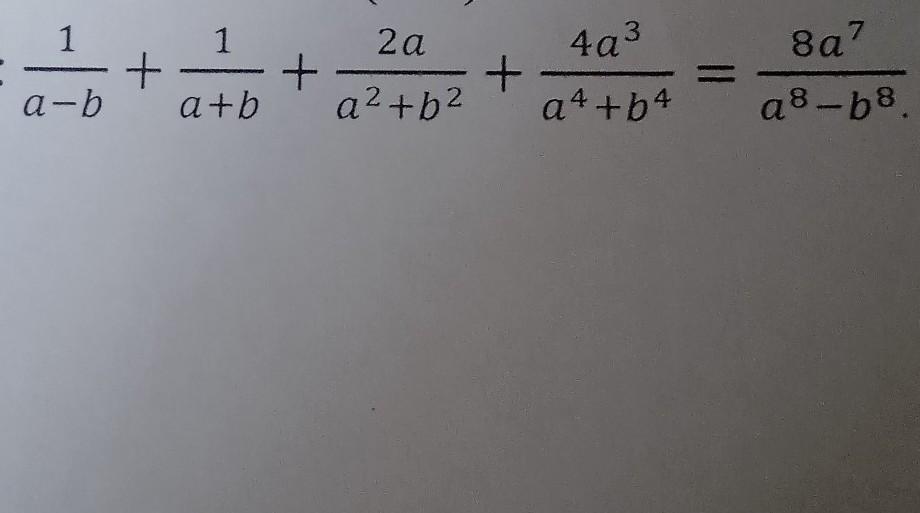
Ответы
Автор ответа:
2
Ответ:
Доказать тождество .
.
Приводим дроби к общему знаменателю. Применяем формулу
разности квадратов :
Тождество доказано .
Приложения:
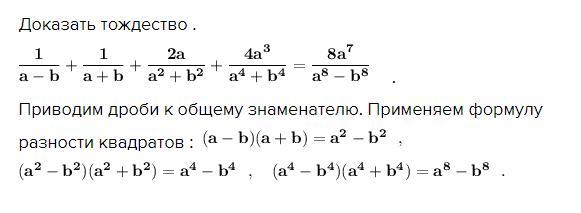

Похожие вопросы
Предмет: Алгебра,
автор: tymurmrinskyi
Предмет: Алгебра,
автор: nekrylovaliza78
Предмет: История,
автор: dominica61
Предмет: Математика,
автор: vinylblood36
Предмет: Литература,
автор: gladkowavika0512