Question

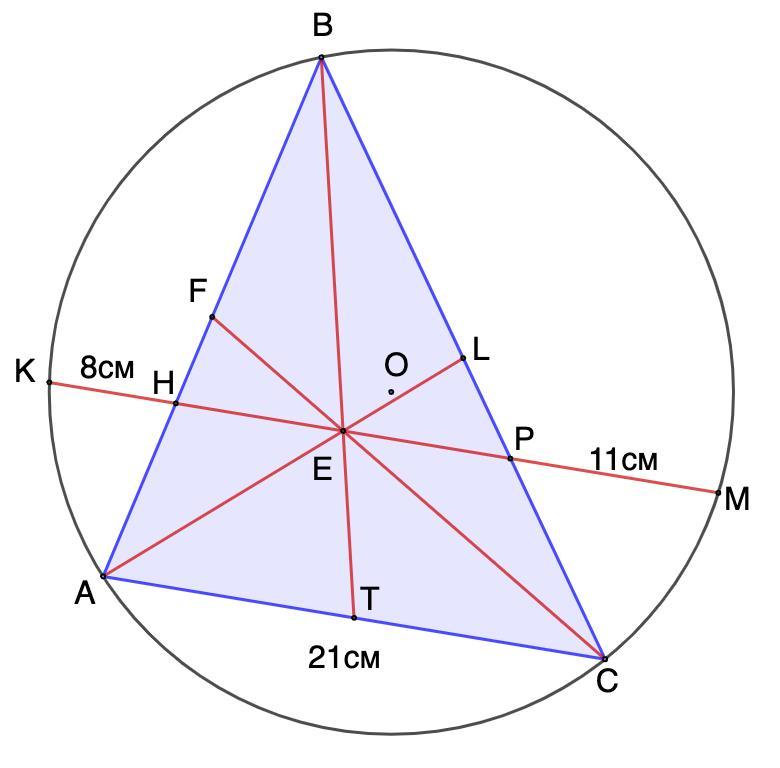
У коло вписано трикутник, одна із сторін якого дорівнює 21 см.
Паралельно цій стороні через точку перетину медіан проведено хорду.
Відрізки хорди, розміщені поза трикутником, дорівнюють 8 см і 11 см.
Знайдіть невідомі сторони трикутника.

Answer 1

Ответ:

Стороны треугольника равны 30 см и 33 см.

Объяснение:

В круг вписан треугольник, одна из сторон которого равна 21 см. Параллельно этой стороне через точку пересечения медиан проведена хорда. Отрезки хорды, расположенные за пределами треугольника, равны 8 см и 11 см.

Найдите неизвестные стороны треугольника.

Дано: ΔАВС;

Окр.О - описана около ΔАВС;

AL ∩ CF ∩ BT = Е - медианы;

КМ || АС;

АС = 21 см; КН = 8 см; РМ = 11 см.

Найти: АВ; ВС.

Решение:

• Медианы треугольника пересекаются в одной точке и делятся точкой пересечения в отношении 2 : 1, начиная от вершины.

⇒ АЕ : ЕТ = 2 : 1.

• Если на одной стороне угла отложить отрезки и через их концы провести параллельные прямые, то на другой стороне угла эти прямые отсекут отрезки, пропорциональные отрезкам на первой стороне.          

⇒ ВН : НА = ВР : РС = 2 : 1.

или ВН : ВА = ВР : ВС = 2 : 3

Рассмотрим ΔНВР и ΔАВС.

∠В - общий.      ВН : ВА = ВР : ВС = 2 : 3

⇒   ΔНВР ~ ΔАВС (по двум пропорциональным сторонам и углу между ними)

Напишем отношения сходственных сторон.

$\displaystyle \frac{HP}{AC}=\frac{BH}{BA}\\ \\ \frac{HP}{21}=\frac{2}{3}\;\;\;\Rightarrow \;\;\;HP=\frac{21\cdot2}{3}=14$   (см)

КМ ∩ ВА = Н   -   хорды.

• Если две хорды окружности пересекаются, то произведение отрезков одной хорды равно произведению отрезков второй хорды.

Пусть АН = х см, тогда НВ = 2х см.

КН = 8 см; НМ = 14 + 11 = 25 см

⇒ АН · НВ = КН · НМ

х · 2х = 8 · 25

2х² = 8 · 25  

х² = 4 · 25  

х = 2 · 5 = 10

⇒ АН = 10 см; НВ = 20 см; АВ = 30 см.

КМ ∩ ВС = Р   -   хорды.

Пусть РС = у см, тогда ВР = 2у см.

РМ = 11 см; РК = 14 + 8 = 22 см

⇒ РС · ВР = РМ · РК

у · 2у = 11 · 22

2у² = 11 · 22  

у² = 11 · 11  

у = 11

⇒ РС = 11 см; ВР = 22 см; АВ = 33 см.

Стороны треугольника равны 30 см и 33 см.

#SPJ1