Предмет: Геометрия,
автор: 5pnsnrk44s
СРОЧЧНОО 40б
Найти площадь закрашенной части круга если угол AOB=120 а радиус =корень из 3
Приложения:
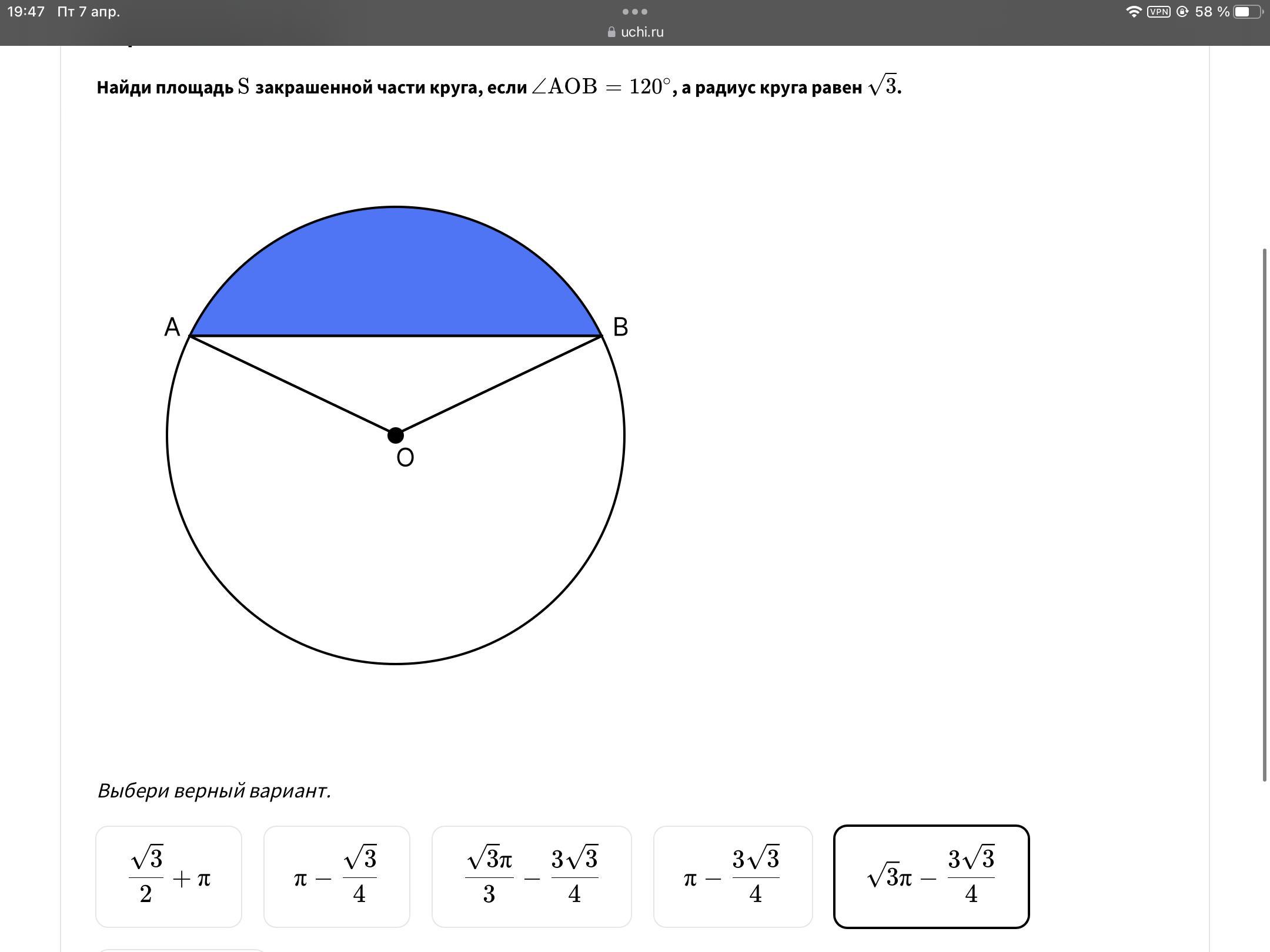
Ответы
Автор ответа:
1
Ответ:
вот решение
Объяснение:
на листочке
Приложения:
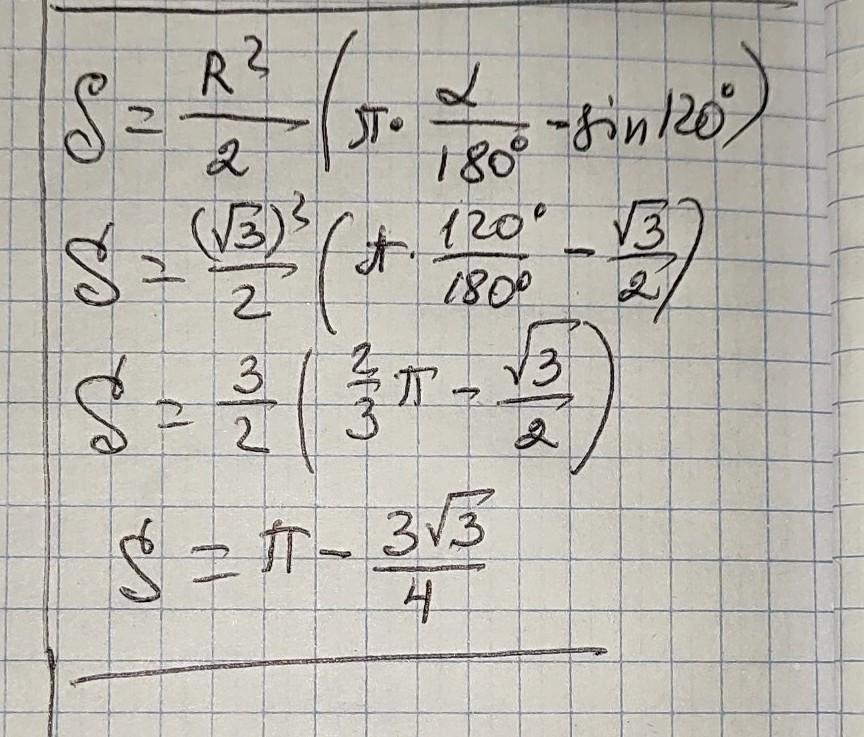
Автор ответа:
1
Ответ:
π -3√3/4
Объяснение:
Поскольку площадь закрашенной части S₍ₐ₎ равна разности площадей кругового сектора АОВ и треугольника АОВ то (для случая, когда величина ∠АОВ выражена в градусах) имеем:
S₍ₐ₎ = πR²α/360° - 1/2 *R²*sinα = ¹/₂ *(πα/180° - sinα)R²
S₍ₐ₎ = ¹/₂ *(π*120°/180° - sin120°)* (√3)²
S₍ₐ₎ = ¹/₂ *(2π/3 - √3/2)*3 = ³/₂ * 2π/3 - ³/₂ * √3/2 = π -3√3/4
Похожие вопросы
Предмет: Алгебра,
автор: kravcenkoesenia007
Предмет: Алгебра,
автор: timotiodessa
Предмет: Биология,
автор: CreckYT
Предмет: Математика,
автор: 01032006soni
Предмет: Биология,
автор: gerasimenkoviktor808