Question

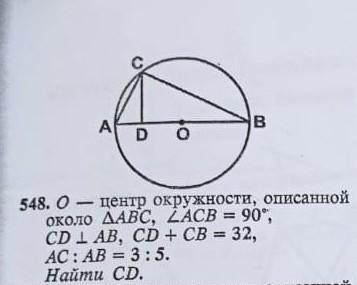
O - центр окружности, описанной Oколо AABC, LACB=90"," CDL AB, CD+ CB = 32, AC: AB=3:5. Найти CD.​

Answer 1

Ответ:

AE/AB = AC/BC

(x - CD)/x = 3x/4x

x - CD = 3x/4

CD = x/4

Также, согласно теореме Пифагора для прямоугольного треугольника ABC, мы имеем:

AC^2 = AB^2 + BC^2

(3x)^2 = x^2 + (4x)^2

9x^2 = 17x^2

x^2 = 9/8

Теперь мы можем выразить CD через x:

CD = x/4 = (1/4) * √(9/8) = (3/8) * √2

Таким образом, CD равен (3/8) * √2.