Предмет: Математика,
автор: kirilukviktoria2
Приклад 2,3, 4. Буду дуже вдячна якщо дасте відповідь до 11:00 години
Приложения:
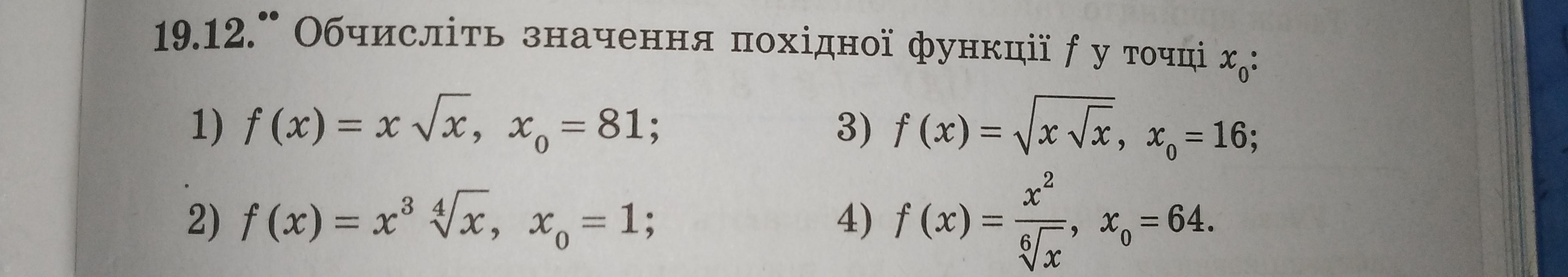
Ответы
Автор ответа:
0
Відповідно до умови задачі, нам потрібно обчислити значення похідної функції у заданій точці. Для цього використаємо формулу похідної диференціюванням функції відносно змінної x:
f(x) = √x, x0 = 81:
f'(x) = 1 / (2 * √x)
f'(81) = 1 / (2 * √81) = 1/18
f(x) = (2x + 5) / (x - 1), x0 = 9/5:
f'(x) = [(x - 1)(2) - (2x + 5)(1)] / (x - 1)^2
f'(9/5) = [(9/5 - 1)(2) - (2(9/5) + 5)*(1)] / (9/5 - 1)^2 = -139/100
f(x) = x^3 - 3x^2 + 2x, x0 = 0:
f'(x) = 3x^2 - 6x + 2
f'(0) = 3(0)^2 - 6(0) + 2 = 2
f(x) = 98^(2-x), x0 = 64:
f'(x) = -ln(98)*98^(2-x)
f'(64) = -ln(98)*98^(2-64) = -ln(98)*98^(-62)
Отже, ми обчислили значення похідних функцій у заданих точках.
f(x) = √x, x0 = 81:
f'(x) = 1 / (2 * √x)
f'(81) = 1 / (2 * √81) = 1/18
f(x) = (2x + 5) / (x - 1), x0 = 9/5:
f'(x) = [(x - 1)(2) - (2x + 5)(1)] / (x - 1)^2
f'(9/5) = [(9/5 - 1)(2) - (2(9/5) + 5)*(1)] / (9/5 - 1)^2 = -139/100
f(x) = x^3 - 3x^2 + 2x, x0 = 0:
f'(x) = 3x^2 - 6x + 2
f'(0) = 3(0)^2 - 6(0) + 2 = 2
f(x) = 98^(2-x), x0 = 64:
f'(x) = -ln(98)*98^(2-x)
f'(64) = -ln(98)*98^(2-64) = -ln(98)*98^(-62)
Отже, ми обчислили значення похідних функцій у заданих точках.
Похожие вопросы
Предмет: Обществознание,
автор: Аноним
Предмет: Українська література,
автор: borovroma87
Предмет: Другие предметы,
автор: guzalniazova805
Предмет: История,
автор: alermo1999
Предмет: Биология,
автор: mobis4685