!15 баллов! Вопрос на фото решение розпишите пожалуйста (спасибо)

Ответы
Відповідь:
1)∠А=30°, АВ=6 см, АС=3√3 см
2)∠В=45°, АВ=8√2 дм, АС=8 дм
3)1)∠А=25°, АВ=10,46 см, ВС=3,07 см
Пояснення:
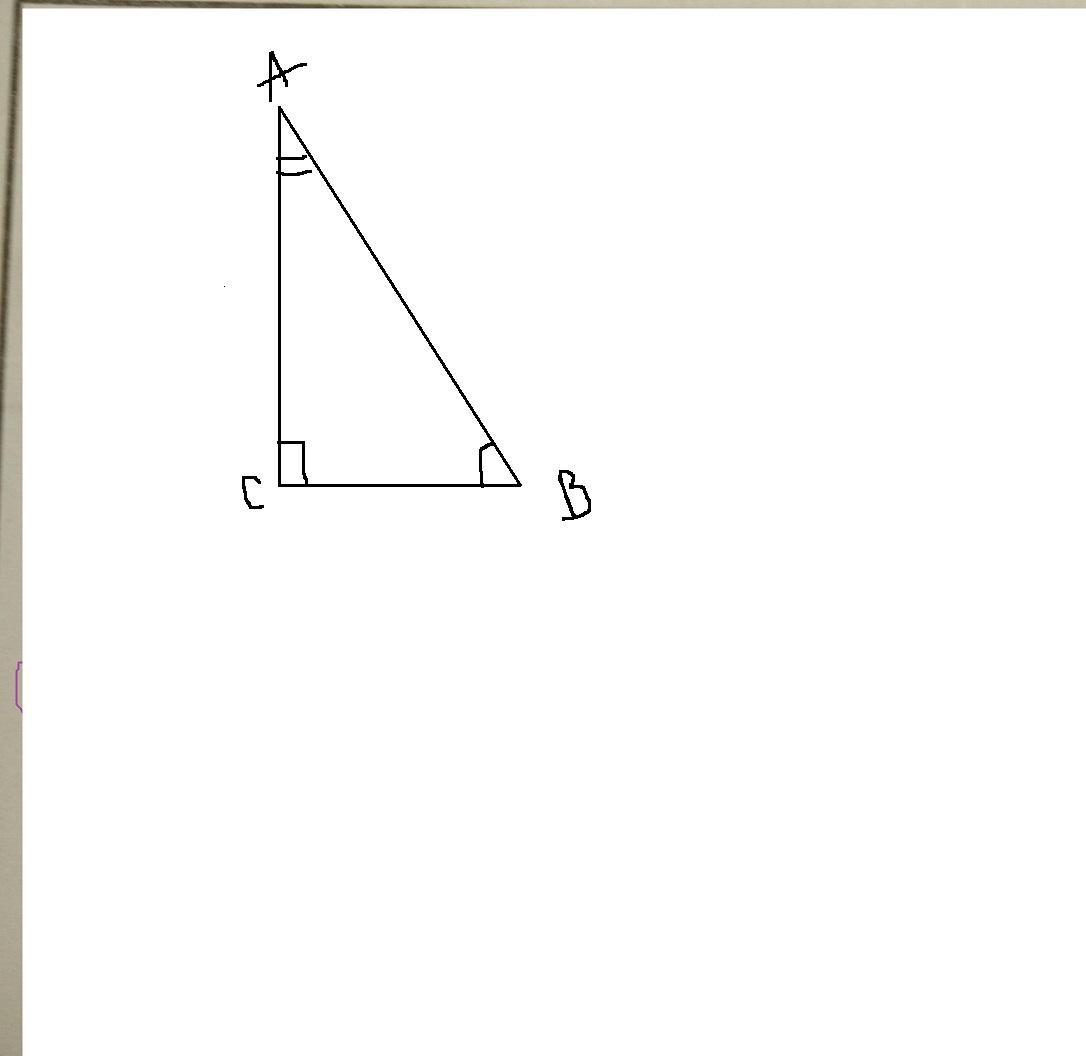
1) Дано: ΔАВС, ∠С=90°, ∠А=60°, ВС=3 см
Знайти:∠В-?, АС, АВ-?
Рішення:
За теоремою про суму гострих кутів прямокутного трикутника
∠А+∠В=90° →∠В=90°-∠А=90°-60°=30°.
За теоремою про катет, що лежить проти кута в 30° ВС=1/2 АВ →
АВ=2ВС=2*3 см=6 см.
За теоремою Піфагора АВ²=ВС²+АС² →АС²=АВ²-ВС² (cм)
2)Дано: ΔАВС, ∠С=90°, ∠В=45°, ВС=8 дм
Знайти:∠А-?, АС, АВ-?
Рішення:
За теоремою про суму гострих кутів прямокутного трикутника
∠А+∠В=90° →∠А=90°-∠В=90°-45°=45°.
ΔАВС- рівнобедрений, так як ∠А=∠В=45°. Отже АС=СВ -за визначенням рівнобедреного трикутника.
За теоремою Піфагора АВ²=ВС²+АС²=2ВС² →(дм).
3)Дано: ΔАВС, ∠С=90°, ∠В=75°, АС=10 см
Знайти:∠А-?, BС, АВ-?
Рішення:
За теоремою про суму гострих кутів прямокутного трикутника
∠А+∠В=90° →∠А=90°-∠В=90°-75°=25°. ,sin 75°≈0,965 ( по таблиці )
АВ=10 : 0,965=10,46 см
За теоремою Піфагора АВ²=ВС²+АС² →ВС²=АВ²-АС²≈3,07 cм