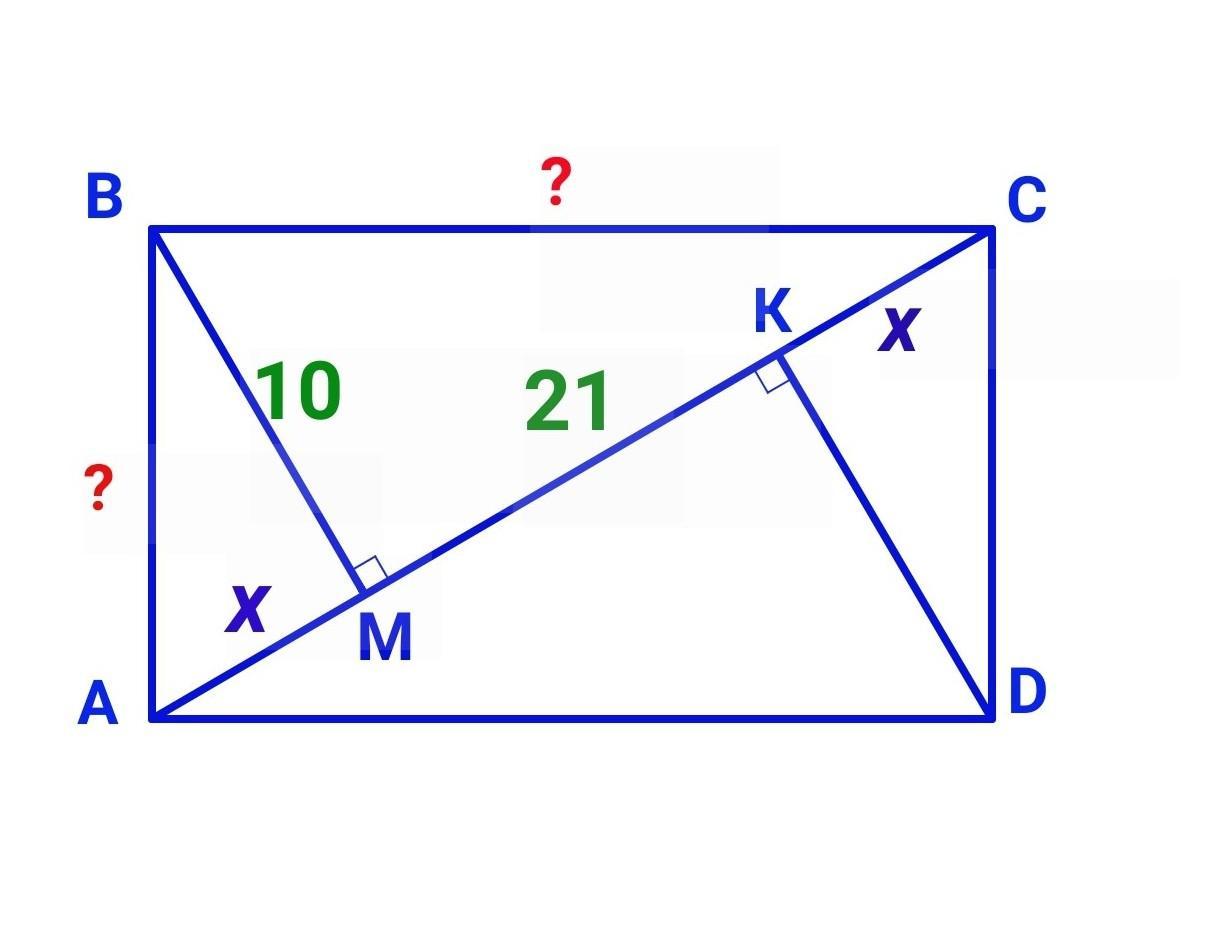
У прямокутнику АВСD до діагоналі АС проведено перпендикуляри ВМ і DK. Відомо, що ВМ=10см, МК= 21 см. Знайдіть сторони прямокутника
Ответы
Ответ: 2√29 см, 5√29 см
Объяснение:
У прямокутнику АВСD до діагоналі АС проведено перпендикуляри ВМ і DK. Відомо, що ВМ=10см, МК= 21 см. Знайдіть сторони прямокутника.
Задано прямокутник ABCD, AC - діагональ, BM⟂AC, DK⟂ AC, BM= 10 см, MK = 21 см
1) Розглянемо прямокутні трикутники АBM і CDK.
- AB=CD - як протилежні сторони прямокутника
- ∠BAM=∠ DCK - як внутрішні різносторонні кути при перетині паралельних прямих AB і CD січною АС.
△ABM=△CDK за гіпотенузою і гострим кутом.
AM=CK - як відповідні сторони рівних трикутників
2) Позначимо АМ =CK =х (см), тоді MC =MK+KC= (21+x) см - за аксиомою вимірювання відрізків.
3) Розглянемо прямокутний трикутник АBC (∠B=90°)
BM - висота, що проведена з вершини прямого кута, тому за метричними співвідношеннями у прямокутному трикутнику маємо:
BM²=AM•MC
10²=х•(21+х)
х²+21х-100=0
За теоремою Вієта отримаємо два корені:
х₁=-25 (не відповідає умові задачі)
х₂=4
Отже, AM =4 (см) , MC=21+4= 25 (см)
4) У прямокутному трикутнику ABM (∠B=90°) за теоремою Піфагора знайдемо гіпотенузу АВ:
AB²= BM²+AM²=10²+4²=116
AB=2√29 (см)
5) У прямокутному трикутнику BMC (∠M=90°) за теоремою Піфагора знайдемо гіпотенузу ВС:
BC ²=BM²+MC²=10²+25²=725
BC=5√29 (см)
Відповідь: так як протилежні сторони прямокутника рівні, то:
AB=CD= 2√29 (см),
BC=AD= 5√29 (см).
#SPJ1