Question

Очень прошу помочь!! Это правда срочно. Заранее спасибо.

Answer 1

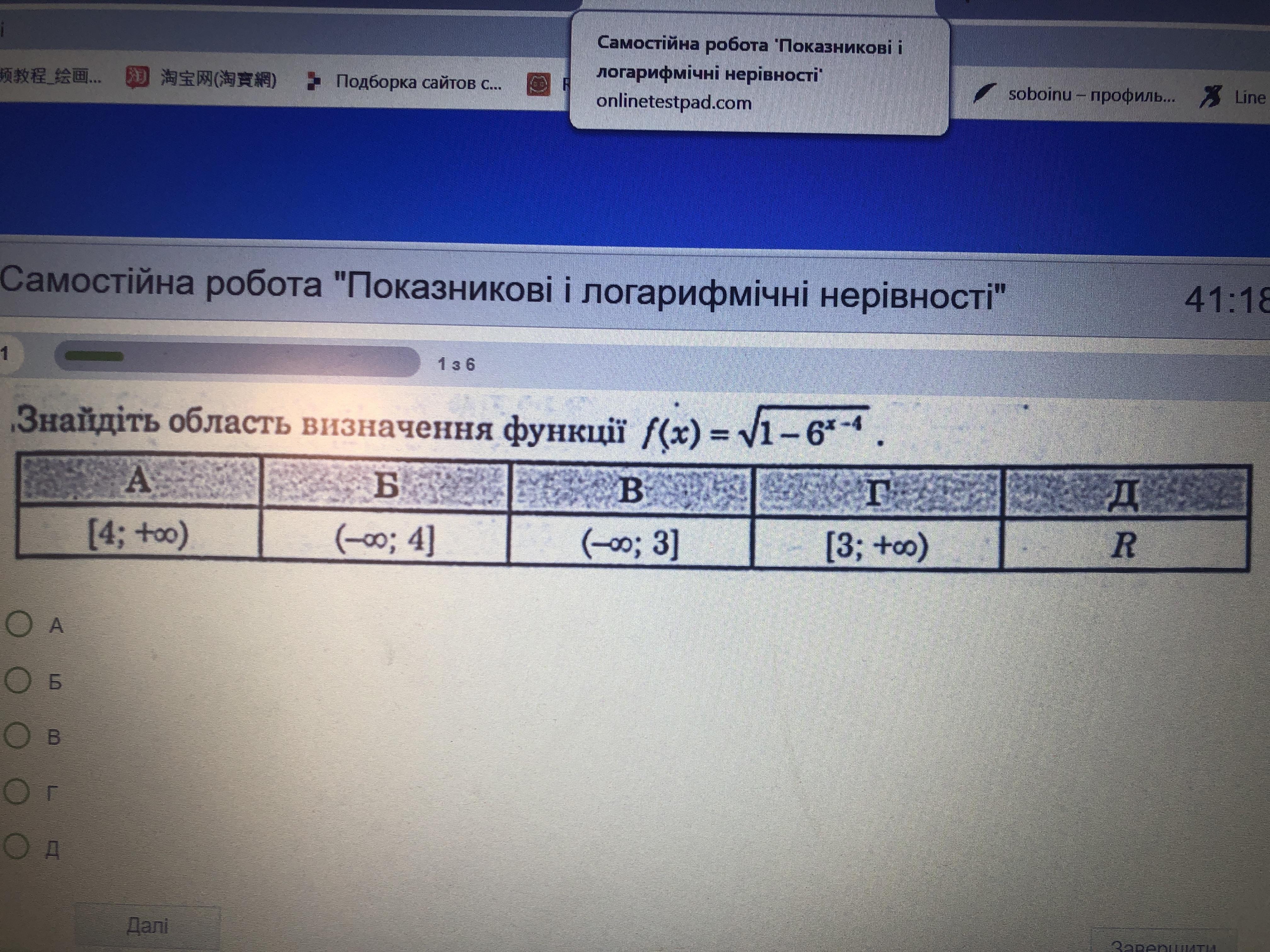
Решение.

  $\bf y=\sqrt{1-6^{^{x-4}}}$

Подкоренное выражение должно быть неотрицательным .

$\bf 1-6^{^{x-4}}\geq 0\ \ ,\\\\6^{^{x-4}}\leq 1\\\\6^{^{x-4}}\leq 6\, ^0$  

Так как показательная функция имеет основание  6>1 , то она возрастающая . Поэтому знак между аргументами останется таким, каким и был между функциями .

$\bf x-4\leq 0\\\\x\leq 4\\\\\boldsymbol{x\in (-\infty \, ;\ 4\ ]}$  

Ответ:  Б) .