Предмет: Алгебра,
автор: Аноним
Помогите с решением пожалуйста интеграл
Приложения:

Ответы
Автор ответа:
1
Ответ:
15) Применяем универсальную тригонометрическую подстановку .
17) В числителе выделяем cosx , чтобы записать выражение cosx dx как дифференциал d(sinx) .
Приложения:

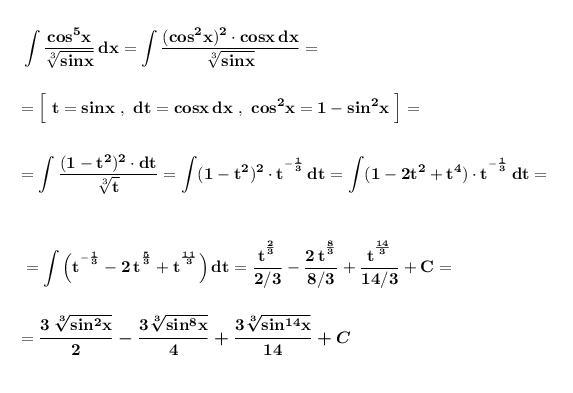
Похожие вопросы
Предмет: Математика,
автор: leralanymi
Предмет: Химия,
автор: pktoto09
Предмет: Физика,
автор: alinurabitai155
Предмет: Химия,
автор: SlS112
Предмет: Математика,
автор: Maschentsy