Предмет: Алгебра,
автор: Аноним
Помогите с решением пожалуйста
интеграл
Приложения:

Ответы
Автор ответа:
1
Ответ:
Замена в интегралах от иррациональных функций .
Разложим дробь на сумму простейших дробей .
14) Запишем подынтегральное выражение как квадратный корень из дроби .
Проинтегрируем по частям .
Приложения:

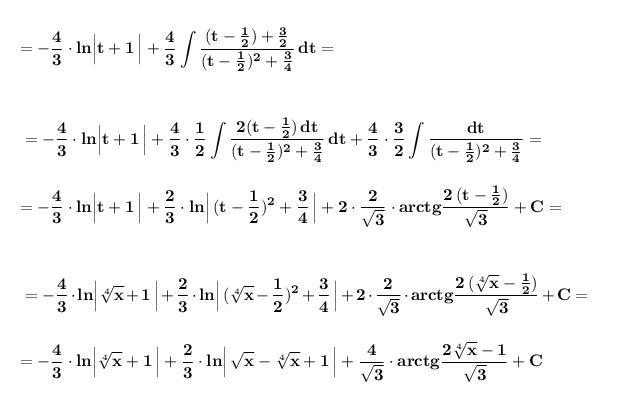

Похожие вопросы
Предмет: Химия,
автор: pktoto09
Предмет: Физика,
автор: alinurabitai155
Предмет: Литература,
автор: danielandreev47
Предмет: Математика,
автор: Maschentsy
Предмет: Алгебра,
автор: alveek48