Question

Задание на фото, нужно только 3,4

Answer 1

Ответ:

Пошаговое объяснение:

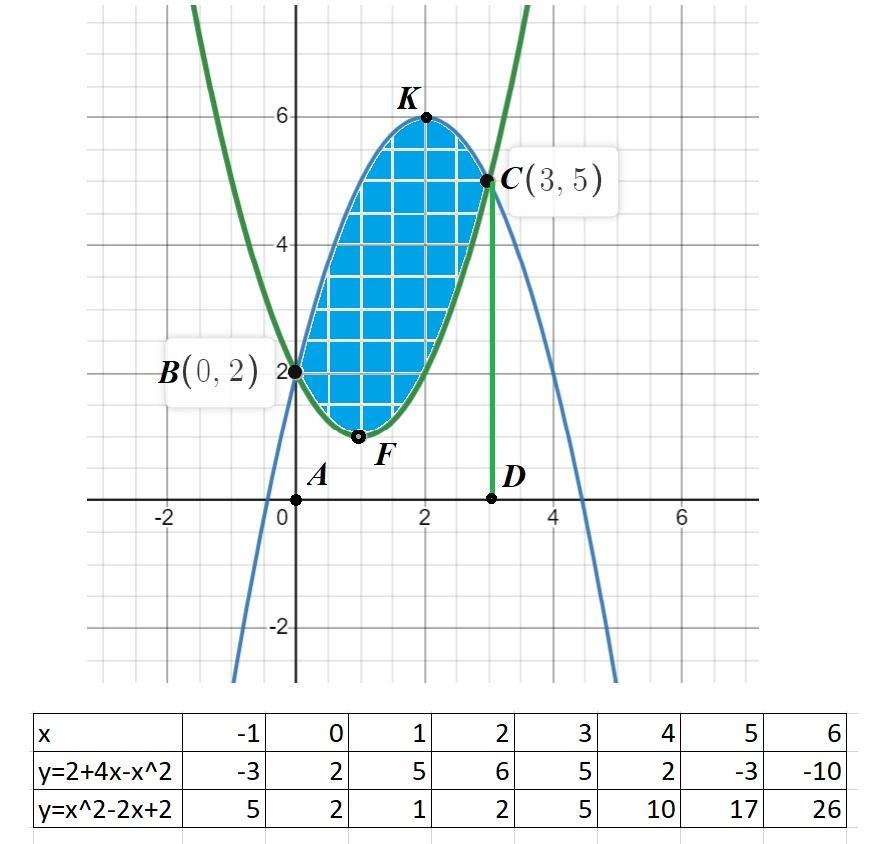
Строим графики функций

y=2+4x-x^2;

y=x^2-2x+2.

S=S(ABKCD) - S(ABFCD);

Площадь находим по формуле Ньютона -Лейбница

S=∫ₐᵇ(F(x))dx =∫ₐᵇf(b)dx -∫ₐᵇf(a)dx=∫ₐᵇ(2+4x-x^2) - ∫ₐᵇ (x^2-2x+2);

По графику находим пределы интегрирования => от 0 до 3.

S = ∫₀³(2+4x-x^2) - ∫₀³(x^2-2x+2) =(2x+2x^2-x^3/3)|₀³ - (x^3/3-x^2+2x)|₀³ =

= (2*3+2*3^2-3^3/3) - (3^3/3-3^2+2*3) = 15-6=9 кв. ед.

*************************

4)  y=x^2-x;  y=3x.

Строим графики и находим пределы интегрирования

(См. скриншот)

S=∫ₐᵇF(x) dx = ∫ₐᵇf(b)dx -∫ₐᵇf(a)dx

По графику определяем пределы интегрирования => от 0 до 4.

S=∫₀⁴3xdx -∫₀⁴(x^2-x)dx = (3x^2/2 - x^3/3 + x^2/2)|₀⁴ = 3*4^2/2-4^3+4^2/2 =

=48/2-64/3+16/2= 32/3 = 10 2/3  кв. ед.