Предмет: Алгебра,
автор: irozvadovskaya2007
Помогите Пожалуйста Срочно Надо!!!
Приложения:
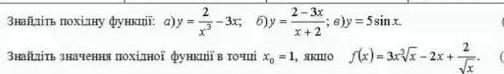
irozvadovskaya2007:
__irina_007
так ты поможешь, да или нет?
Ответы
Автор ответа:
0
Ответ:
1) Производную функции находим, применяя правила дифференцирования и таблицу производных .
2)
Похожие вопросы
Предмет: Английский язык,
автор: kreculliana24
Предмет: Математика,
автор: mandarin8642
Предмет: Литература,
автор: olakylbeda2010
Предмет: Биология,
автор: MiliyKrolik092
Предмет: Математика,
автор: timurnazhmetdinov033