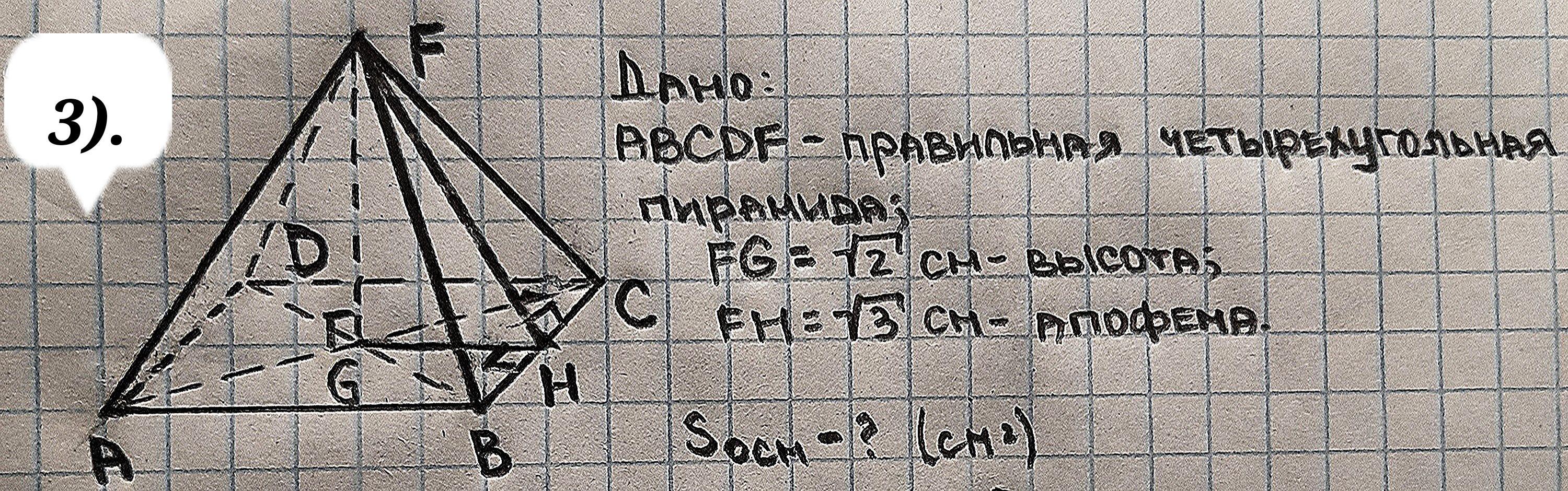Геометрия даю 100 баллов

Ответы
Ответ:
3. Площадь основания равна 4 см².
4. Площадь боковой поверхности правильной треугольной усеченной пирамиды равна 72 см².
Объяснение:
3. Найти площадь основания правильной четырехугольной пирамиды, высота которой составляет √2 см, если ее апофема равна √3 см.
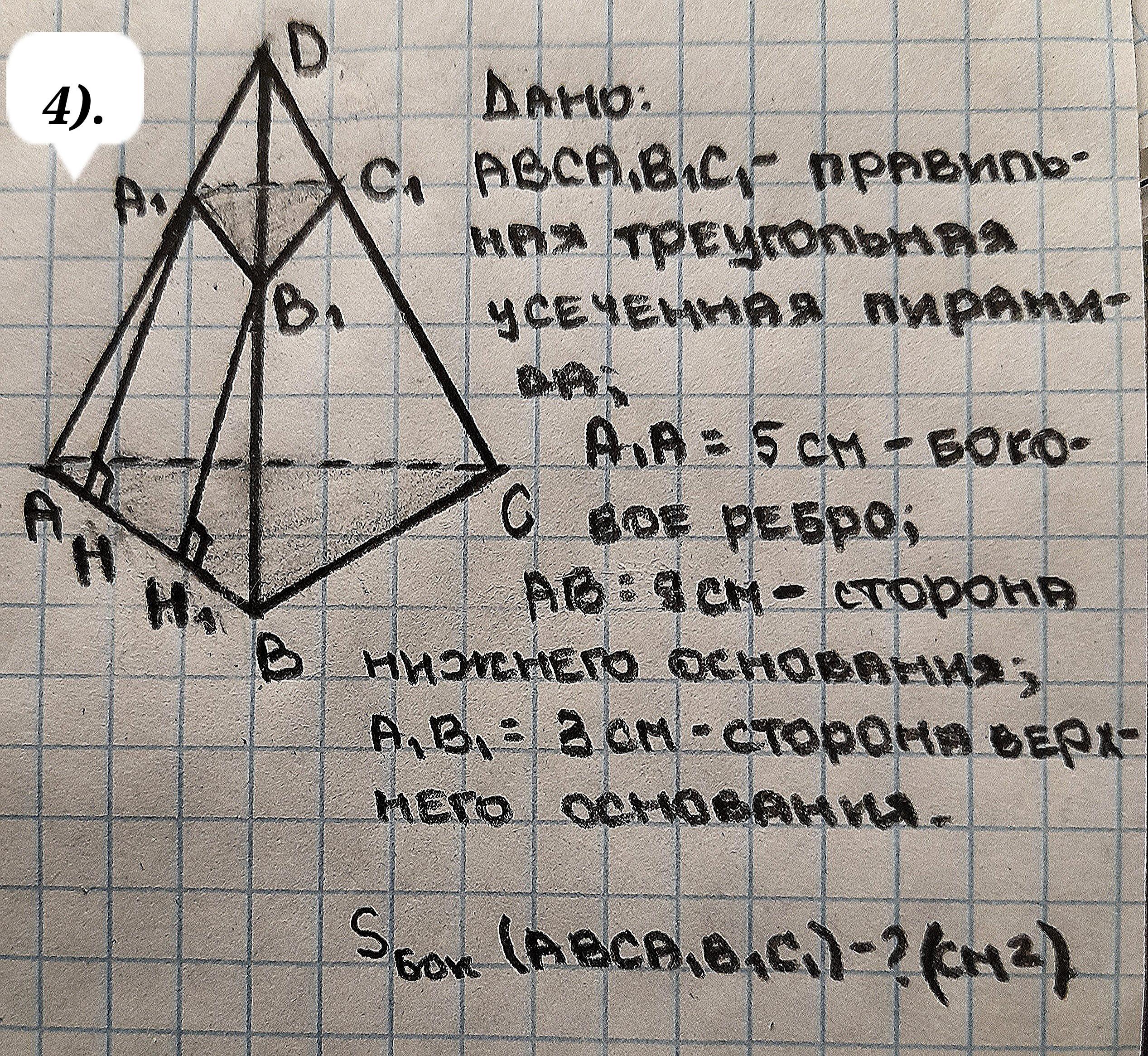
4. Найти площадь боковой поверхности правильной треугольной усеченной пирамиды, если ее боковое ребро равно 5 см, а стороны оснований составляют 3 см и 9 см.
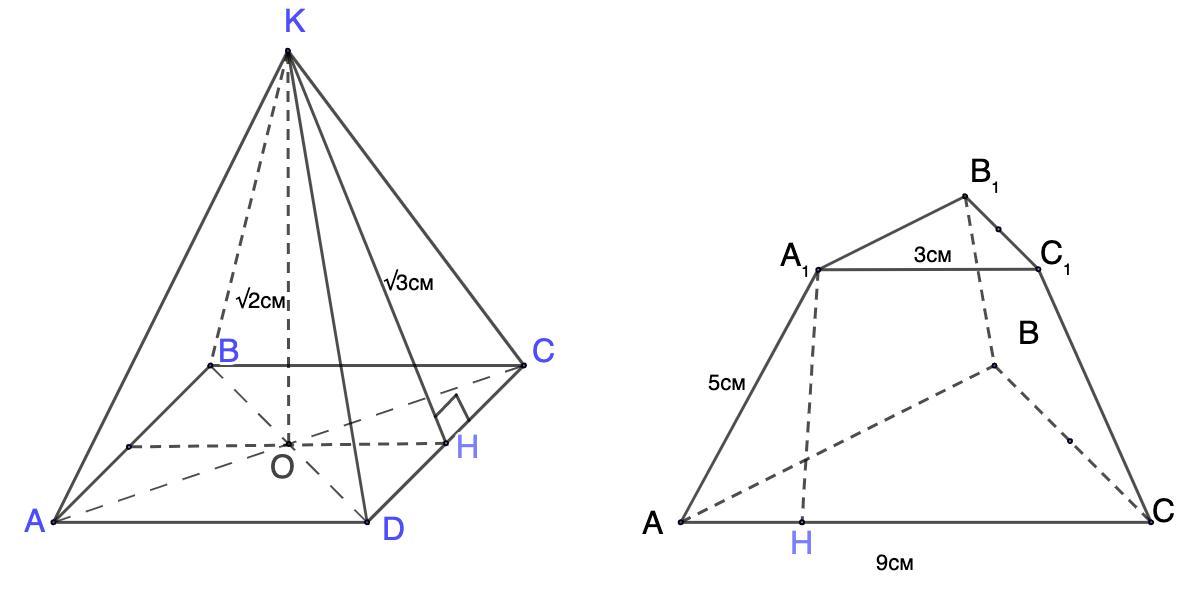
3. Дано: KABCD - правильная четырехугольная пирамида;
КО = √2 см - высота; КН = √3 см - апофема.
Найти: Sосн.
Решение:
Соединим Н и О.
- В основании правильной четырехугольной пирамиды лежит квадрат, а боковые грани - равнобедренные треугольники.
Рассмотрим Δ DKC - равнобедренный.
КН ⊥ DC (KH - высота)
- В равнобедренном треугольнике высота, проведенная к основанию, является медианой.
⇒ DH = HC.
Рассмотрим ΔОКН - прямоугольный.
По теореме Пифагора:
OH² = KH² - OK² = 3 - 2 = 1 ⇒ OH = 1 см.
Рассмотрим ΔАСD.
DH = HC
- Диагонали квадрата точкой пересечения делятся пополам.
⇒ АО = ОС
⇒ ОН - средняя линия.
- Средняя линия равна половине стороны, которую она не пересекает.
⇒ AD = 2 · 1 = 2 (см)
- Площадь квадрата равна квадрату его стороны.
⇒ S осн. = 2² = 4 (см²)
Площадь основания равна 4 см².
4. Дано: АВСA₁B₁C₁ - правильная треугольная усеченная пирамида.
АА₁ = 5 см; А₁С₁ = 3 см; АС = 9 см.
Найти: S бок.
Решение:
- В правильной треугольной усеченной пирамиде основания - правильные треугольники, а боковые грани - равнобедренные трапеции.
⇒ АА₁С₁С - равнобедренная трапеция.
Проведем высоту А₁Н.
- Высота, проведенная из вершины тупого угла равнобедренной трапеции к большему основанию, делит его на части, меньшая из которых равна полуразности оснований.
⇒ АН = (АС - А₁С₁) : 2 = (9 - 3) : 2 = 3 (см)
Рассмотрим ΔАА₁Н - прямоугольный.
По теореме Пифагора:
А₁Н² = АА₁² - АН² = 25 - 9 = 16 ⇒ А₁Н = 4 см.
- Площадь боковой поверхности правильной усеченной пирамиды равна:
S бок. = 1/2 (Р₁ + Р₂) · l ,
где Р₁ и Р₂ - периметры оснований, l - апофема.
Р₁ = 3 · 3 = 9 (см); Р₂ = 9 · 3 = 27 (см)
S бок. = 1/2 (9 + 27) · 4 = 72 (см²)
Площадь боковой поверхности правильной треугольной усеченной пирамиды равна 72 см².
Ответ:
3) 4 см²;
4) 72 см².
Объяснение:
задание 3.
найти площадь основания правильной четырехугольной пирамиды, высота которой составляет √2 см, если ее апофема равна √3 см.
___________________________________
дано:
ABCD - правильная четырехугольная пирамида;
FG=√2 см - высота;
FH=√3 см - апофема.
найти:
- ? (см²)
___________________________________
решение:
правильная четырехугольная пирамида - многогранник, состоящий из четырех боковых граней - равнобедренных треугольников, равных между собой, и из основания - правильного четырехугольника (квадрата).
высота правильной четырехугольной пирамиды проецируется в центр ее основания.
апофема правильной четырехугольной пирамиды - высота ее боковой грани.
пусть ABCDF - правильный четырехугольная пирамида, FG - ее высота, FH - ее апофема.
- рассмотрим треугольник FHG, он прямоугольный, поскольку FG - высота пирамиды. по теореме Пифагора квадрат гипотенузы равен сумме квадратов катетов, следовательно, FH²=FG²+GH² ⇒
- рассмотрим треугольник BGC, он равнобедренный, поскольку диагонали квадрата равны и точкой пересечения делятся пополам. тогда GH - высота данного треугольника, и, поскольку высота пирамиды проецируется в центр основания, AB=2*GH=2*1=2 см.
- найдем площадь квадрата - основания правильной четырехугольной пирамиды, она равна квадрату его стороны:
ответ: площадь основания правильной четырехугольной пирамиды составляет 4 см².
задание 4.
найти площадь боковой поверхности правильной треугольной усеченной пирамиды, если ее боковое ребро равно 5 см, а стороны оснований составляют 3 см и 9 см.
___________________________________
дано:
ABCA₁B₁C₁ - правильная треугольная усеченная пирамида;
A₁A=5 см - боковое ребро усеченной пирамиды;
AB=9 см - сторона нижнего основания;
A₁B₁ = 3 см - сторона верхнего основания.
найти:
- ? (см²)
___________________________________
решение:
правильная треугольная пирамида - многогранник, состоящий из трех боковых граней - равнобедренных треугольников, равных между собой, и из основания - правильного треугольника.
правильная усеченная треугольная пирамида - многогранник, являющийся нижней частью полной правильной треугольной пирамиды, образовавшейся в результате среза вершины данной пирамиды плоскостью, параллельной основанию.
- пусть ABCD - правильная треугольная пирамида, A₁B₁C₁ - плоскость, параллельная основанию и отсекающая вершину D данной пирамиды. тогда АА₁=5 см - боковое ребро усеченной пирамиды, AB=9 см и A₁B₁=3 см - стороны ее оснований.
- рассмотрим боковую грань усеченной пирамиды - равнобедренную трапецию AA₁B₁B. проведем равные высоты A₁H и B₁H₁ (они равны апофеме усеченной пирамиды), тогда прямоугольные треугольники A₁HA и B₁BH₁ равны по гипотенузе и острому углу (AA₁=BB₁ как боковые стороны равнобедренной трапеции, ∠A₁AH = ∠B₁BH₁ как углы при основании равнобедренной трапеции), следовательно, AH=H₁B как соответствующие элементы равных треугольников. тогда
- найдем апофему HA₁ усеченной пирамиды. рассмотрим треугольник A₁HA. по теореме Пифагора,
- площадь боковой поверхности правильной усеченной пирамиды рассчитывается по формуле
, где P₁ и P₂ - периметры оснований, h - апофема. подставляем:
ответ: площадь боковой поверхности правильной треугольной усеченной пирамиды составляет 72 см².