Предмет: Алгебра,
автор: malajncimaks
Обчислити площу фігури , обмеженої лініями f(x)=-x^2+9, y=0, x=1; x=2
Ответы
Автор ответа:
1
Ответ: 6 2/3 кв. ед.
Объяснение:
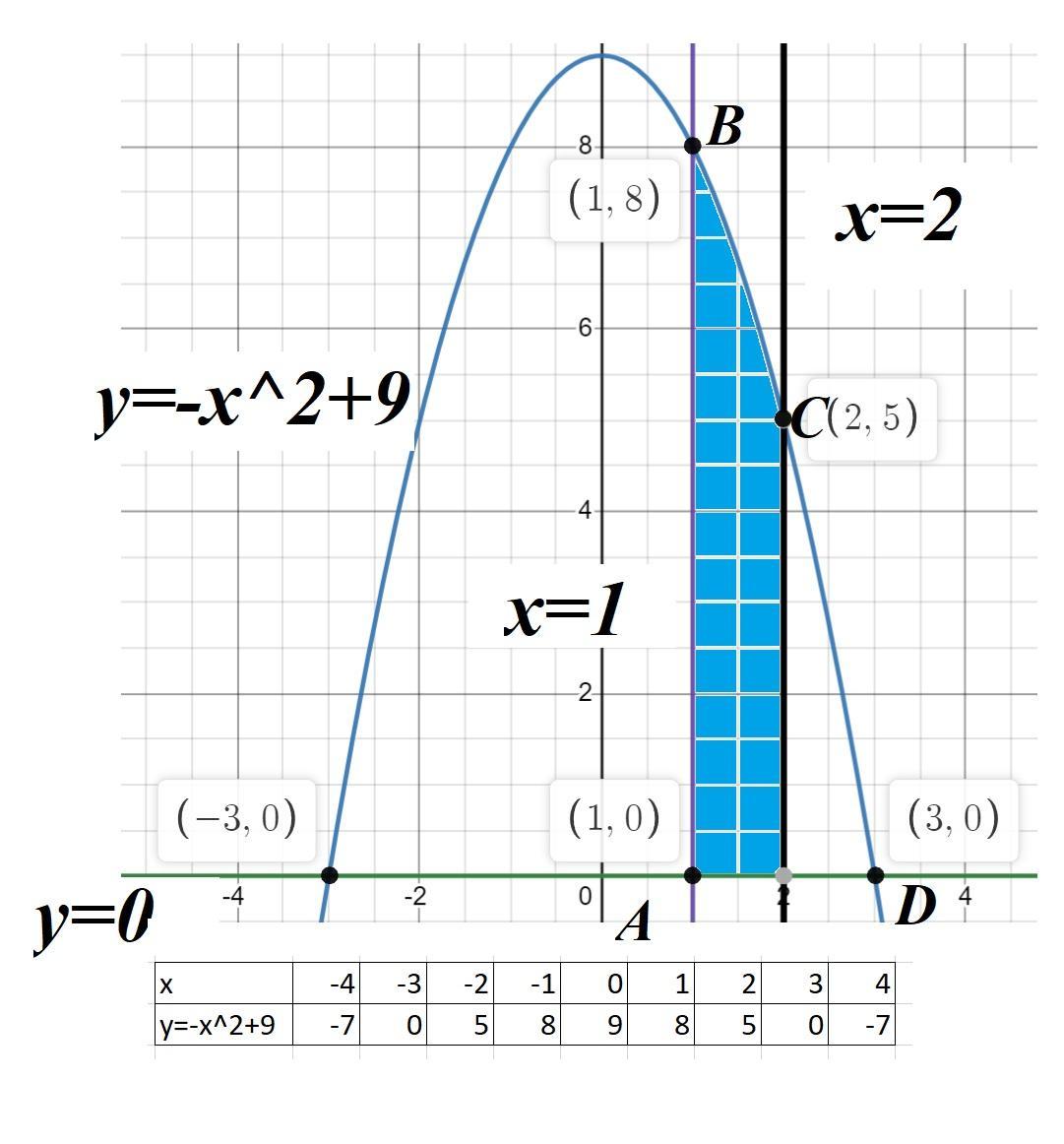
Обчислити площу фігури , обмеженої лініями
y=-x^2+9; y=0, x=1; x=2. (См. скриншот).
Применяем формулу Ньютона-Лейбница
S=S(ABCD) = ∫ₐᵇ(f(x)) dx.
Пределы интегрирования от x=1 до x=2.
S= ∫₁²(-x²+9)dx - ∫₁²(0)dx = ∫₁²(-x²+9)dx = (9x-x³/3)|₁² = 9x|₁² - x³/3|₁²=
=9(2-1) - 1/3(2³-1³) = 9 - 7/3 = 20/3 = 6 2/3 кв. ед.
Приложения:
ildar502020:
Выберите количество звездочек и оцените ответ
Похожие вопросы
Предмет: Геометрия,
автор: miracleanastasiya
Предмет: Математика,
автор: vodo4ca62
Предмет: Другие предметы,
автор: Pon832
Предмет: Биология,
автор: yana56104
Предмет: Математика,
автор: bromadyk