Предмет: Алгебра,
автор: veronikamila65
Помогите с решением пожалуйста
Приложения:
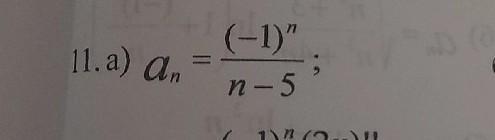
Ответы
Автор ответа:
1
Ответ:
Сходится.
Объяснение:
где
(при n>5).
Применим признак Лейбница, который формулируется так: если
1)
2)
то ряд сходится.
Нам, правда, надо писать первое условие начиная с но это не мешает пользоваться признаком Лейбница:
Итак, начинаем проверять условия признака Лейбница. Пусть n>5; надо доказать, что Для этого рассмотрим разность
Теперь доказываем, что предел равен нулю:
Вывод: по признаку Лейбница наш ряд сходится.
veronikamila65:
спасибо большое
я добавила примеры которые не понимаю, посмотрите тоже пожалуйста
я вас жду, пожалуйста
Похожие вопросы
Предмет: Геометрия,
автор: Onwisjq
Предмет: Музыка,
автор: varamatveeva
Предмет: Физика,
автор: jack2009
Предмет: Музыка,
автор: uakuzmina566
Предмет: Математика,
автор: lidashevhenko1988