Предмет: Алгебра,
автор: Рус55с56к98и15й
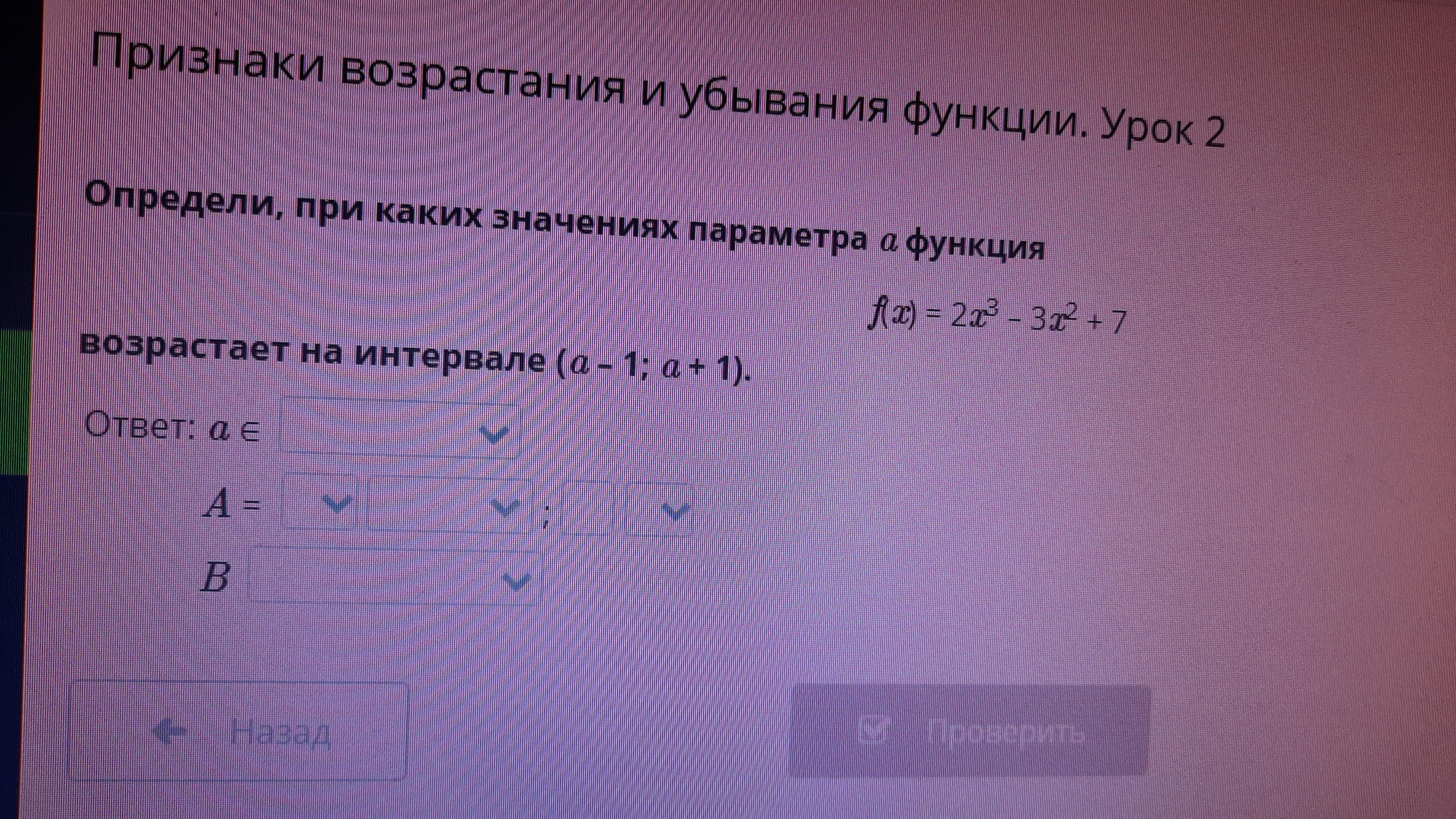
определи при каких значениях параметра а функция f(x)=2x3-3x2+7
Приложения:
Ответы
Автор ответа:
0
Ответ и Объяснение:
Нужно знать: Если производная от функции f(x) положительна на интервале M, то функция возрастает на этом интервале.
Решение. Вычислим производную от функции:
f'(x) = (2·x³ - 3·x² + 7)' = 2·(x³)' - 3·(x²)' + (7)' = 2·3·x² - 3·2·x + 0 = 6·x² - 6·x.
Находим множество, в котором f'(x) > 0, то есть
6·x² - 6·x > 0 ⇔ x·(x - 1) > 0 ⇒ x ∈ (-∞; 0) ∪ (0; +∞).
Но граничные значения интервалов (-∞; 0) и (0; +∞) содержат ∞, то этих интервалов невозможно представить в виде (a-1; a+1).
#SPJ1
Похожие вопросы
Предмет: Русский язык,
автор: simonyaneva69
Предмет: Геометрия,
автор: snejwife
Предмет: Математика,
автор: yqertdcx
Предмет: История,
автор: slavik22858
Предмет: Русский язык,
автор: Аноним