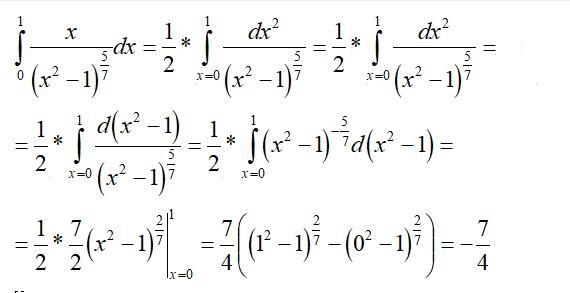Сходиться или расходиться данный интеграл?
integral x/(x^2-1)^(5/7) from 0 to 1
Ответы
Ответ:
Для того, чтобы определить, сходится или расходится данный интеграл, можно воспользоваться признаком сходимости интеграла от неотрицательной функции. Если интеграл от неотрицательной функции сходится, то исходный интеграл тоже сходится, и наоборот, если интеграл от неотрицательной функции расходится, то исходный интеграл тоже расходится.
Рассмотрим функцию f(x) = x/(x^2-1)^(5/7). Поскольку f(x) неотрицательна на отрезке [0, 1], то интеграл от нее существует в несобственном смысле, если он сходится на этом отрезке.
Применим признак сходимости интеграла от неотрицательной функции. Для этого рассмотрим функцию g(x) = f(x)/(x^(2/7)), которая также неотрицательна на отрезке [0, 1].
Тогда
g(x) = x/(x^2-1)^(5/7) / (x^(2/7))
= x^(5/7) / (x^2-1)^(5/7)
Поскольку на отрезке [0, 1] функция g(x) непрерывна, то для того, чтобы интеграл от нее сходился, необходимо и достаточно, чтобы интеграл от g(x) сходился на этом отрезке.
Для проверки сходимости интеграла от g(x) воспользуемся интегральным признаком сходимости:
Если функция f(x) непрерывна, неотрицательна и убывает на бесконечности, то интеграл от нее сходится тогда и только тогда, когда сходится интеграл от функции g(x) = f(x)/x.
Функция g(x) = x^(5/7) / (x^2-1)^(5/7) является неотрицательной и убывает на бесконечности, поскольку
g'(x) = (3x^2 + 2)/(7x^3(x^2-1)^(12/7)) < 0
для всех x > 1.
Таким образом, интеграл от f(x) сходится, и следовательно, исходный интеграл
integral x/(x^2-1)^(5/7) from 0 to 1
также сходится
Пошаговое объяснение:
ЗДЕЛАЙ ПОЖАЛУЙСТА ЛУЧШИЙ ОТВЕТ
Відповідь:
Покрокове пояснення:
integral x/(x^2-1)^(5/7) dx (х from 0 to 1) =
1/2 * integral 1/(x^2-1)^(5/7) d(x^2)(х^2 from 0 to 1) =
1/2 * integral 1/(t-1)^(5/7) dt (t from 0 to 1) =
1/2 * integral 1/(t-1)^(5/7) d(t-1) (t from 0 to 1) =
1/2 * integral 1/y^(5/7) dy (y from -1 to 0) =
1/2 * 7/2 * y^(2/7) (y from -1 to 0) = - 7/4